6.3 Ejemplos con teoría de juegos
En este apartado se presentan algunos ejemplos significativos, que han resultado ser base de diversos modelos para ejemplificar algunas situaciones, que de otra forma pueden resultar insuficientes y no con la claridad que esta teoría muestra.
Este modelo presenta características y resultados que explican, en algún modo, los estados de poco bienestar que podemos observar en diversas situaciones a nuestro alrededor.
6.3.1 Equilibrio de Nash
El equilibrio de Nash es un concepto fundamental en la teoría de juegos, que se utiliza como un método para predecir el resultado de una interacción estratégica. Es el concepto de solución más aplicado en diversos modelos económicos, como son el oligopolio, equilibrio de mercado, problemas de agentes; en política, votaciones, política internacional, tratados, entre muchos otros. Un juego, ya sea en forma estratégica o forma normal, consiste en tres elementos: el conjunto de jugadores, el conjunto de acciones disponibles a cada jugador (estrategias puras) y una función de pagos, que trata de representar de la mejor forma posible, las preferencias de los jugadores sobre las distintas acciones. Un equilibrio de Nash en estrategias puras es un conjunto de acciones con la propiedad de que ningún jugador individual puede obtener un pago más alto si se desvía en forma unilateral de esta acción.
De forma matemática:
Se supone que cada jugador en el juego tiene un número finito de estrategias disponibles, si se designan los n jugadores por \(a1, …, an,\) y si, \((s1, …, sn)\) es el vector de estrategias, cuando cada jugador elige la estrategia si, habrá un pago para el jugador \(j\), que depende de las estrategias que hayan elegido todos los otros los jugadores y se denota por \(Pj (s1, …sn)\) (que puede ser un pago esperado en el caso de juego con elementos de azar).
De forma matemática lo anterior se expresa de la siguiente forma:
El pago para el jugador i, que para cualquier otra estrategia ri se cumple que
\(Pj (s1, s2,…, si,…, sn) \geq Pj(s1, s2,…ri,.., sn)\)
De esta forma se llega a la siguiente definición; Un vector de n entradas \((s1, s2, … sn)\) es un punto de equilibrio en estrategias puras, si la desigualdad anterior se cumple para todos los jugadores i y para cualquier elección de ri dentro del conjunto de estrategias del jugador i.
6.3.2 El dilema del prisionero
El juego conocido como El dilema del prisionero representa el juego más conocido, y el que de alguna forma dio a conocer la importancia de la Teoría de Juegos en diversas disciplinas. Muchos juegos tienen nombres propios, es el caso para este juego y también es el juego más popular para un juego de suma diferente de cero, dos jugadores y dos estrategias. Este juego tiene, un sólo equilibrio de Nash, como veremos más adelante. El dilema surge porque los pagos que los jugadores obtienen en ese equilibrio no son los mejores. Es una situación inferior de Pareto ya que hay otra situación en donde ambos jugadores estarían mejor, en el cual se demuestra que no siempre la decisión racional lleva a un mejor resultado.
Albert W. Tucker es el autor de la paradoja del Dilema del Prisionero la cual sirve para ilustrar la dificultad de analizar los juegos que no son de suma cero. Esta sencilla paradoja ha dado lugar a una amplia literatura en diferentes áreas como la filosofía, biología, ciencia política y economía, así como la propia Teoría de juegos.
Dos agentes que pueden elegir entre cada una de dos acciones: Cooperar (C) o traicionar (D). si ambos agentes eligen C, cada agente obtiene un pago (recompensa) R; Si uno defrauda mientras que el otro coopera, el primero consigue el pago T (con T> R, mientras que el último consigue un pago de consolación S (con S< R; pero si ambos traicionan, ambos obtienen un pago P. Con las restricciones estándar T >R > P > S, T+P < 2R, la traición es la mejor elección en un simple juego, es decir es el equilibrio de Nash.
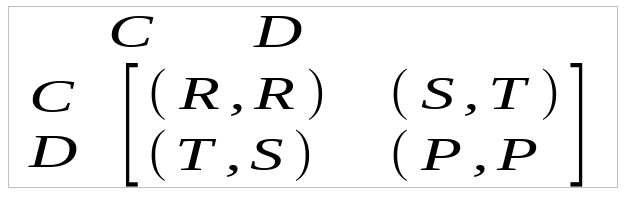
En este juego, el peor resultado que pueden obtener los jugadores cuando uno de los jugadores traiciona (D, C) 0 (C, D)), y el otro jugador coopera, y es este punto el que hace que ambos jugadores elijan (D, D), ambos traicionar, obteniendo un pago menor que el que obtendrían si ambos cooperan (C, C) dado que el riesgo de perder aún más es incierto.
Siempre es posible repetir los juegos, y entonces observar diferentes comportamientos dependiendo de las estrategias que elijan cada uno de los participantes. Es muy conocido el concurso llevado a cabo por Axelrod, en donde los jugadores pueden ir construyendo sus estrategias dependiendo de los resultados y del comportamiento de los otros jugadores.
El modelo iterado de DP para dos personas como se muestra a continuación demuestra un concepto interesante: al interactuar con otros jugadores a lo largo del tiempo en un escenario de dilema del prisionero, y hay posibilidades de ajustar su estrategia para que funcione bien con la de ellos. Cada estrategia posible tiene fortalezas y debilidades únicas que aparecen a lo largo del juego. Por ejemplo, la estrategia de traicionar siempre produce el mejor resultado cuándo los otros jugadores eligen aleatoriamente sus estrategias, pero se obtiene el peor resultado cuándo los otros jugadores también eligen traicionar, a esta situación se le puede llamar Ojo por ojo.
Esto hace que sea difícil e interesante determinar una única "mejor" estrategia. Uno de esos enfoques para hacer esto es crear un mundo con múltiples agentes que juegan una variedad de estrategias en situaciones repetidas del dilema del prisionero.
6.3.3 Juego iterado del Dilema del prisionero
Un modelo basado en agentes representa una sociedad artificial integrada por agentes autónomos, y heterogéneos, que interactúan entre sí y con el ambiente bajo reglas sencillas de decisión. Los agentes al evaluar su situación y evolucionar pueden presentar comportamientos emergentes. Estos modelos constituyen una metodología para el estudio de la complejidad social a través del modelado y la simulación computacional en el estudio de las organizaciones y la dinámica de sistemas.
Este modelo realizado con el programa NetLogo (Wilensky, 2002), el cual ya se explicó en el capítulo anterior, supone que un aumento en el número de personas que cooperan aumentará proporcionalmente el beneficio para cada jugador que coopera. Para aquellos que no cooperan, el pago que obtienen es un factor (alfa) multiplicado por el número de personas que cooperan. En un dilema del prisionero iterado con múltiples jugadores, se puede observar la dinámica de la evolución en la cooperación.
Para que el lector pueda experimentar con las dinámicas del modelo del DP, se le proporciona el link del simulador implementado en NetLogo Web: http://www.complejidad.iiec.unam.mx/libro/capitulo6/GICE_DPI_espacial2022.html
6.3.3.1 Elementos del modelo
El elemento principal del modelo del DPI es la matriz de pagos, la cual tiene la siguiente estructura:
| Jugador B | |||
| Jugador A | Coopera | Traiciona | |
| Coopera | (1,1) | (0, ALFA) | |
| Traiciona | (ALFA, 0) | (0,0) | |
(x, y) = x: puntaje del jugador A, y: puntaje del jugador B. Entre mayor es el puntaje (beneficio que obtienen), es mejor.
Matriz de pagos: ALFA = premio a la traición (Defection-Award,) varía en un rango de 0 a 3. Al Presionar SETUP se puede observar que los parches rojos (que traicionan) y los parches azules (cooperarán) están dispersos a lo largo del archivo. Al presionar GO se inicia las iteraciones para que los parches interactúen con sus ocho parches vecinos. Al inicio se cuentan el número de parches vecinos que están cooperando. Si un parche está cooperando, entonces su puntaje es el número de parches vecinos que también cooperaron. Si un parche está traicionando, entonces su puntaje es el producto del número de parches vecinos que están cooperando, multiplicado por el valor de ALFA.
¿En la siguiente ronda, el parche establecerá su antigua estrategia de cooperar? Dado que fue la estrategia que usó en la ronda anterior. Para la próxima ronda, el parche adoptará la estrategia de uno de sus vecinos que obtuvo la puntuación más alta en la ronda anterior.
Si un parche es azul, entonces el parche cooperó en la ronda anterior y actual. Si un parche es rojo, entonces el parche desertó en la iteración anterior, así como en la ronda actual. Si un parche es verde, entonces el parche cooperó en la ronda anterior, pero desertó en la ronda actual. Si un parche es amarillo, entonces el parche desertó en la ronda anterior, pero cooperó en la ronda actual.
A continuación, se muestran algunos resultados.
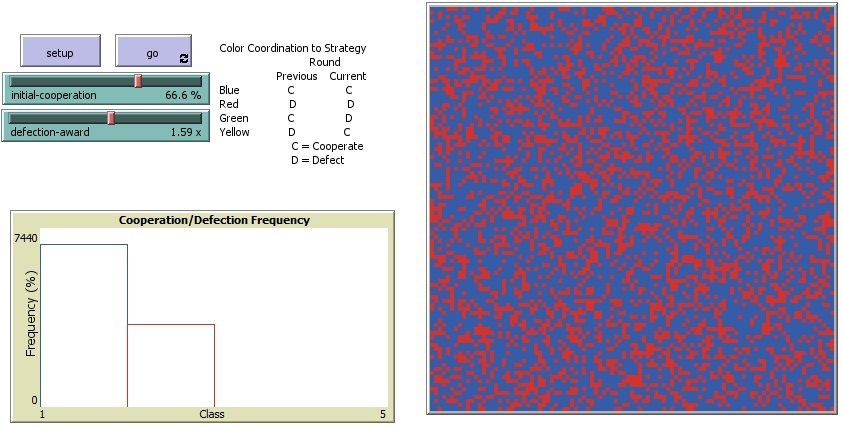
Figura 1. Pantalla inicial de la interfaz del juego en NetLogo.
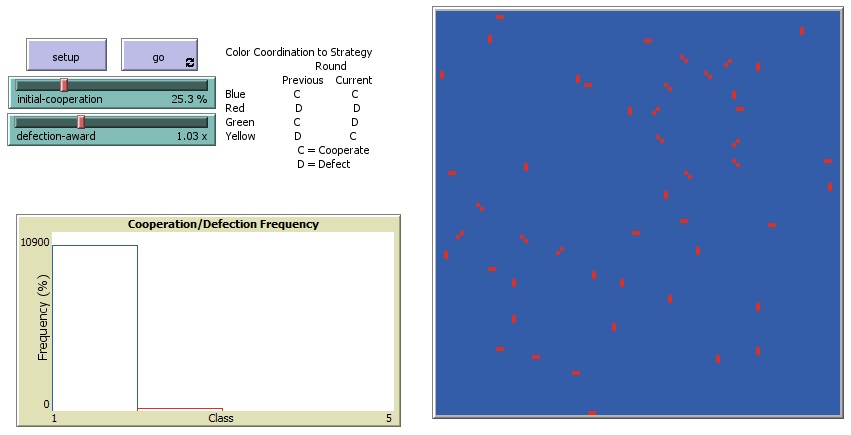
Figura 2. Resultados de la evolución del juego con initial-cooperation = 25.3% y defection-award = 1.03x.
En la Figura 2, los valores del premio a la traición son de 1.03, y el porcentaje inicial de jugadores cooperadores de 25.3%. El resultado que se observa es una mayoría cooperadora, color azul, y algunos jugadores que traicionan, color rojo.
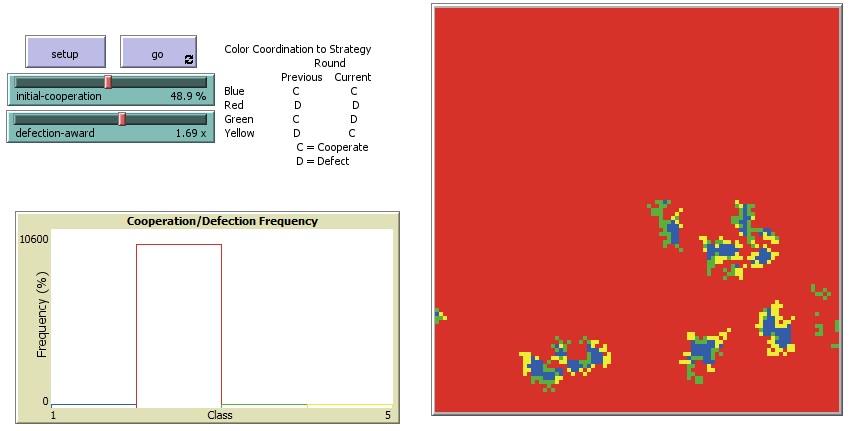
Figura 3. Resultados de la evolución del juego con initial-cooperation = 48.9% y defection-award = 1.69x.
En este caso, los valores del premio a la traición son de 1.69x, y el porcentaje inicial de jugadores cooperadores de 48.9%. El resultado que se observa es una mayoría traidora, color rojo, y algunos jugadores con estrategias coopera y luego traiciona, y algunos de color amarillo, que primero traicionan y luego cooperan.
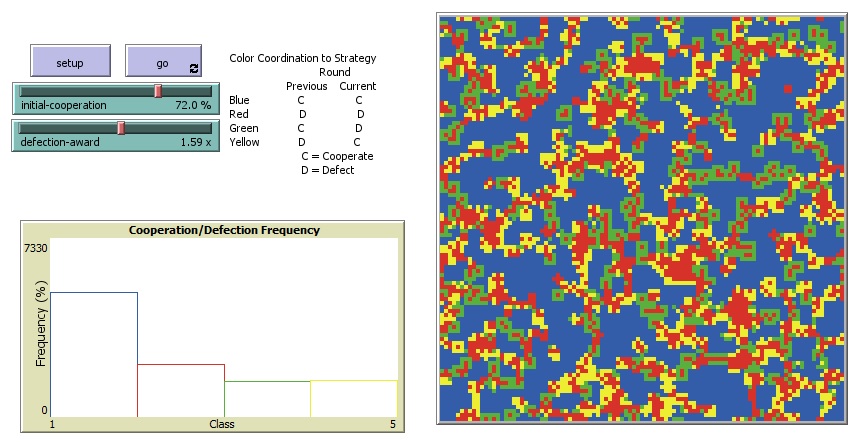
Figura 4. Con la variación de parámetros se pueden obtener patrones con estructuras interesantes, por ejemplo, con initial-cooperation = 72% y defection-award = 1.59x, hay jugadores en rojo (DD), con vecindades de jugadores en verde (CD), y prevalecen los jugadores cooperadores en azul. Estos patrones son inestables espacialmente, ya que cambian sus estados repetidamente, pero el histograma (como medida estadística) permanece estable de manera cualitativa.
6.3.3.2 Propuestas para modificar el modelo
Se propone modificar el código para que los parches tengan una estrategia para implementar. Por ejemplo, en lugar de adoptar para cooperar o traicionar en función del parche vecino con la puntuación máxima. En cambio, deje que cada parche considere la historia de cooperación o traición sus parches vecinos, y permita que decida si cooperar o traicionar como resultado.
Implemente estas cuatro estrategias:
- Coopere todo el tiempo: independientemente del historial de parches vecinos, coopere.
- Ojo por ojo: solo coopere con parches vecinos, si nunca han traicionado. De lo contrario, traicione.
- Ojo por ojo con perdón: cooperar si en la ronda anterior, el parche cooperó. De lo contrario, traicionar.
- Traicionar todo el tiempo: independientemente del historial de parches vecinos, traiciono.
Preguntas
¿Cómo se distribuyen los parches cooperantes y desertores? ¿Qué estrategia resulta con la puntuación más alta en promedio? ¿En qué condiciones estas estrategias no tendrán una resultante, estado final con la mayoría cooperadora? ¿Para qué valor de ALFA un parche será indiferente a traicionar o cooperar
6.3.4 El conflicto entre los intereses individuales y eluso de los recursos comunes
En otro enfoque es importante analizar los modelos en los cuales hay un conflicto entre los intereses individuales y el uso de recursos comunes, a través de la teoría de juegos, en donde las decisiones individuales racionales afectan de manera negativa a la sociedad generando resultados indeseables para todos. El ejemplo clásico es el propuesto por el biólogo Garret Hardin en 196812: la tragedia de los comunes:
“Imagine un pastizal abierto para todos. Es de esperarse que cada pastor intentará mantener en los recursos comunes tantas cabezas de ganado como le sea posible. (...) Como un ser racional, cada pastor busca maximizar su ganancia. Explícita o implícitamente, consciente o inconscientemente, se pregunta, ¿cuál es el beneficio para mí de aumentar un animal más a mi rebaño? Esta utilidad tiene un componente negativo y otro positivo.
- El componente positivo es una función del incremento de un animal. Como el pastor recibe todos los beneficios de la venta, la utilidad positiva es cercana a +1.
- El componente negativo es una función del sobrepastoreo adicional generado por un animal más. Sin embargo, puesto que los efectos del sobrepastoreo son compartidos por todos los pastores, la utilidad negativa de cualquier decisión particular tomada por un pastor es solamente una fracción de -1.
Al sumar todas las utilidades parciales, el pastor racional concluye que la única decisión sensata para él es añadir otro animal a su rebaño, y otro más... Pero esta es la conclusión a la que llegan cada uno y todos los pastores sensatos que comparten recursos comunes. Y ahí está la tragedia. Cada hombre está encerrado en un sistema que lo impulsa a incrementar su ganado ilimitadamente, en un mundo limitado. La ruina es el destino hacia el cual corren todos los hombres, cada uno buscando su mejor provecho en un mundo que cree en la libertad de los recursos comunes. La libertad de los recursos comunes resulta la ruina para todos."
6.3.4.1 Ejemplo numérico, y el equilibrio de Nash
Los campesinos Ignacio y José dejan pastar sus borregos en el mismo pastizal que no pertenece a ninguno de los dos, (esto se conoce como bien común). Si hay 20 borregos pastando juntos en el campo, ya sea de uno de los campesinos o de los dos, cada borrego producirá 50 Kg de lana durante un año. Si hay más de 20 borregos, cada borrego tiene acceso a menos pasto y la producción de lana disminuye. Con 30 borregos en el campo, cada borrego producirá 35 Kg de lana, y con 40 borregos producirá cada uno sólo 25 Kg. Cada borrego cuesta $200 y cada campesino puede sólo comprar 10 o 20 borregos. El kilogramo de lana se vende a $100. Los pagos se muestran en la siguiente tabla:
| Ingreso en $
x1000 |
José | ||
| Ignacio | Comprar 10 | Comprar 20 | |
| Comprar 10 | (48,48) | 33, 66) | |
| Comprar 20 | (66,33) | (46,46) | |
De la tabla podemos observar que el equilibrio de Nash se alcanza cuándo los dos jugadores deciden comprar 20 borregos cada uno, ya que desviarse de forma unilateral de esa estrategia los llevaría al riesgo de ganar menos. Sin embargo, la solución, comprar 10 borregos obtiene el mejor pago para los dos jugadores.
6.3.5 Juego del halcón y la paloma
Este es un ejemplo que se utiliza para introducir las ideas de evolución en el contexto de la teoría de juegos.
Dos aves de la misma especie compiten por un territorio (Cuyo valor es el valor de sobrevivencia denotado por V). Las estrategias de comportamiento de cada ave son dos: se pueden comportar de forma pasiva (paloma), o bien de forma agresiva (halcón). Si ambos se comportan como paloma se dividen el territorio y cada uno obtiene V/2. Si uno se comporta como halcón y el otro como paloma, el halcón se queda con todo el territorio, gana, y el que juega como paloma no gana nada. Si ambos se comportan como halcón habrá un enfrentamiento, una pelea, cuyo valor negativo es C., y el pago que obtiene es W dado por
W = (1/2)V - C
Donde C es el valor de la pelea. Si consideramos que ambas aves tienen la misma probabilidad de ganar la pelea, y por lo tanto el territorio. Se deben analizar dos casos posibles:
Caso 1: V = 6 y C = 2. (Caso dilema del prisionero). Este caso representa un valor de la pelea pequeño comparado con el valor de la recompensa.
| P | H | |
| P | (3,3) | (0*,6*) |
| H | (6*,0) | (1*,1*) |
El asterisco muestra la mejor estrategia para los dos jugadores; cuando ambos coinciden se obtiene la solución de equilibrio, que como se muestra no es la mejor solución.
Caso 2: V=6 y C=6. (Caso juego la gallina). En este caso el valor de la pelea es comparable con el valor de recompensa. De esta forma se obtiene la siguiente matriz de pagos:
En el primer caso, siguiendo el procedimiento descrito, si el ave 1 muestra alguna señal de que se va a comportar como paloma, el ave 2, para maximizar su bienestar elegirá comportarse como halcón, ya que es mejor 6 que 3; pero si el ave 1 muestra una señal de que se va a comportar como halcón, el jugador 2, entre obtener 0 o 1, elegirá el 1, o sea halcón. De forma análoga para el ave 1, entre ganar 3 o 6, es mejor 6, por lo que elige halcón; pero si el otro jugador da señales de comportarse como halcón, entre ganar 0 o 1, elegirá halcón de nuevo. Este razonamiento nos lleva a considerar que (halcón, halcón) es la estrategia de equilibrio debido a que, si alguno de los dos se desvía de ella, obtendrá un resultado peor. La solución (paloma, paloma) les reporta un mejor pago a los dos jugadores, sin embargo, no es posible que cualquiera de ellos tome el gran riesgo que representa elegir esa estrategia, por lo que no es una solución.
En el caso dos, la pelea puede ser muy costosa, puede incluso ser mortal, por lo que las condiciones del juego cambian. Este caso, si el otro jugador da una señal de comportarse como halcón, lo mejor es elegir paloma y de esta forma evitar la pelea. Este es un juego con dos equilibrios: (halcón, paloma) y (paloma, halcón). Por lo que el juego tiene un tercer equilibrio en estrategias mixtas. 1 Lo que significa que no hay una estrategia determinada para jugar, sino que se debe determinar una forma que combine las dos estrategias. Los pesos, o frecuencias de cada estrategia elegida se obtienen se pueden obtener por el método de las curvas de reacción que se verán más adelante. El matemático J. Nash, (1950) demostró que todo juego en el cual el conjunto de acciones disponibles a cada jugador es finito, tiene al menos un equilibrio en estrategias mixtas. Que exista una multiplicidad de equilibrios ha permitido que se desarrolle una amplia discusión para identificar los criterios para elegir el equilibrio apropiado. Sin embargo, el equilibrio de Nash representa, algunas veces, una solución que es ineficiente, en el sentido de que existen alternativas que son factibles, y que todos los jugadores las preferirían.
6.3.5.1 Estrategias mixtas para el juego del halcón y la paloma
| P | H | |
| P | (3,3) | (0*,6*) |
| H | (6,0*) | (-3,-3) |
En la matriz anterior se identificaron dos equilibrios de Nash, que fueron obtenidos por estrategias puras. De acuerdo con la teoría del equilibrio de Nash en estrategias puras, sí tenemos un numero impar de estrategias puras, tenemos un tercer equilibrio por estrategias mixtas. Determine utilizando las curvas de reacción para este juego.
6.3.5.2 Estrategias mixtas para un juego de dos personas de suma diferente de cero
Dada la siguiente matriz de pagos para un juego de dos personas A y B cada uno con dos estrategias: Determine utilizando las curvas de reacción para este juego.
Para la matriz de pagos siguiente:
| \(B_1\) | \(B_2\) | |
| \(A_1\) | (\(a _{21},b_{12})\) | (\(a _{12},b_{12})\) |
| \(A_2\) | (\(a _{21},b_{21})\) | (\(a _{22},b_{22})\) |
El pago esperado que obtiene cada jugador al utilizar las estrategias mixtas \(X\) = (\(x_1, x_2\)) con \(x_1 + x_2 = 1\), y \(x_2 = 1 –x_1\), eliminado una variable siempre podemos escribir las estrategias mixtas como \(X = (x, 1-x)\), y \(Y = (y, 1-y)\) son:
$$ E_a(x,y)=\begin{pmatrix} X & 1-X \end{pmatrix} \begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} y\\ 1-y \end{pmatrix} $$
Y para el jugador B:
$$ E_b(x,y)=\begin{pmatrix} X & 1-X \end{pmatrix} \begin{pmatrix} b_{11} & b_{12}\\ b_{21} & b_{22} \end{pmatrix} \begin{pmatrix} y\\ 1-y \end{pmatrix} $$
De donde se obtienen las siguientes expresiones:
\(E_A = ((a_{11}x + a_{21}(1-x))y + (a_{21}x + a_{22}(1-x(1-y)))\)
\(E_A = ((b_{11}x + b_{21}(1-x))y + (b_{21}x + b_{22}(1-x(1-y)))\)
Es importante escribir estas expresiones de la siguiente forma: para el jugador A de debe factorizar con respecto al
valor de “x” para resaltar la forma funcional de este pago con su propia elección, y para el jugador B se debe factorizar con respecto a “y”, obteniendo:
\(E_A = x[(a_{11} - a_{12} - a_{21} + a_{22})y + (a_{12} - a{22})] + [(a_{21} - a_{22}y + a_{22})]\)
\(E_B = y[(b_{11} - b_{12} - b_{21} + b_{22})x + (b_{21} - b{22})] + [(b_{12} - b_{22}y + b_{22})]\)
Los valores de las curvas están en el cuadrado [0,1] x [0,1] en el plano \(xy\). Este plano representa el conjunto de pagos que se pueden obtener para todos los valores de x y y. La gráfica para el jugador A, \(G_A\), se dibuja de la siguiente forma: para cualquier valor “y” fijo, el pago que obtiene EA tendrá la forma de una función lineal EA = mx + c
Donde \(m = ((a_{11} –a_{12}- a_{21} + a_{22})y + (a_{12}-a_{22})\) y \(c = ((a_3-a_4)y + a_4))\). Pero el jugador A no conoce el valor “y” que jugará B, no obstante, sólo hay tres posibilidades para la pendiente \(m\), y todas dependen de la elección del jugador B. Esto hace que el jugador sólo pueda elegir el valor de x que más le convenga:
Si \(m = ((a_{11} –a_{12}- a_{21} + a_{22})y + (a_{12}-a_{22})\geq 0\) entonces el máximo se alcanza en \(x =1\);
Si \(m = ((a_{11} –a_{12}- a_{21} + a_{22})y + (a_{12}-a_{22}) \leq 0\), entonces el máximo se alcanza en \(x = 0\),
Y si \(m = ((a_{11} –a_{12}- a_{21} + a_{22})y + (a_{12}-a_{22}) = 0\) entonces todos los valores de x entre 0 y 1 son máximos.
La gráfica para el jugador A, GA consiste en todos los puntos (x, y) que corresponden a los tres casos de los valores de m. Supongamos ahora que \(X^* = (x^*, 1-x^*)\) y \(Y^* = (y^*, 1-Y^*)\) forman un equilibrio de Nash, entonces por definición este valor estará en la gráfica GA.
Las curvas de reacción para el jugador 1 son:
El pago esperado jugador 1, \(E_1(x,y) = (x)(-6y+3)+9y-3 \) lo que implica que:
| si \(-6y + 3) > 0\) | yo jugador A elegir \(x=1\) |
| si \(-6y + 3) < 0\) | yo jugador A elegir \(x=0\) |
| si \(-6y + 3) = 0\) | yo jugador A elegir \(0 < x < 1\) |
El pago esperado jugador 2, \(E_2(x,y) = (y)(-6x+3) +9x-3\) lo que implica que:
| si \(-6y + 3) > 0\) | yo jugador B elegir \(y=1\) |
| si \(-6y + 3) < 0\) | yo jugador B elegir \(y=0\) |
| si \(-6y + 3) = 0\) | yo jugador B elegir \(0 < y < 1\) |
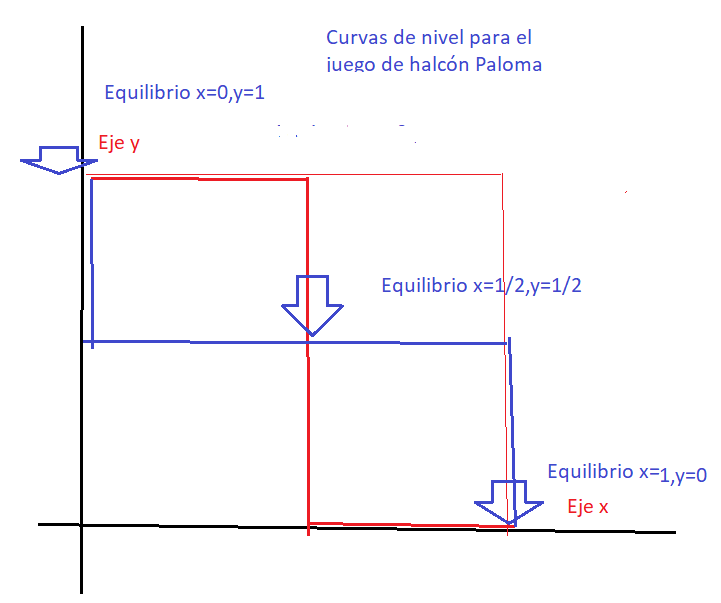
Figura 6. Curvas de reacción para los jugadores y los tres equilibrios de Nash. Dos en estrategias puras y uno en estrategias mixtas.
6.3.6 El juego de la gallina
En este juego dos personas conducen sus autos muy rápido uno hacia el otro en una calle recta. Si alguno de las dos giras y sale de la calle antes que el otro, se le llama gallina (forma coloquial de referirse a una persona cobarde). Por supuesto que, si ninguno gira los autos chocarán. El pago peor que obtienen los jugadores es chocar entre ellos, así que se le asigna el valor -10. Lo mejor que le puede pasar a un jugador, es que el otro gire antes, así que obtiene el pago de 3. Lo siguiente que les puede pasar es comportarse como el gallina con una ganancia de 1. Por último, si ambos se comportan como gallina, entonces como ninguno perdió el honor comportándose como gallina reciben un pago mejor igual a 2.
La matriz de pagos es la siguiente:
| Jugador B | |||
| Jugador A | Girar | Seguir recto | |
| Girar | (2,2) | (1,3) | |
| Seguir recto | (3,1) | (-10,-10) | |
A diferencia del dilema del prisionero, la mutua traición (seguir recto) es el peor resultado. Ambos jugadores quieren hacer lo opuesto de lo que su oponente hace. Los equilibrios de Nash en Estrategias puras son: (seguir recto, girar) u (girar, seguir recto).
Encuentre las estrategias de Nash para el juego de la gallina.