3.1 Introducción
3.1.1 Breve historia de la teoría de sistemas dinámicos
La teoría de sistemas dinámicos ofrece un conjunto de herramientas que permiten estudiar propiedades asociadas con la dinámica, temporal y espacial, de un fenómeno de carácter natural o social. Para ello, se proponen modelos matemáticos que representan los aspectos de mayor interés a estudiar del fenómeno. Su origen se remonta a los trabajos de Newton, quien inventó las ecuaciones diferenciales al expresar matemáticamente su segunda ley: la fuerza es igual a la masa por la aceleración (Madrid, 2011). Una ecuación diferencial se caracteriza por el hecho de que su solución es una función que expresa el ritmo de cambio de una magnitud. Con base en esta idea, Euler sentó las bases de lo que se conoce hoy en día como dinámica clásica a partir de las leyes de Newton y con aplicaciones a partículas y sólidos rígidos (Fernández, 2005). Una peculiaridad del estudio de la dinámica en el contexto de la mecánica clásica es la idea de que la modelización de un sistema dinámico se basa en ecuaciones diferenciales lineales, es decir, aquellas en las que ni su función incógnita ni su derivada están elevadas a una potencia diferente de cero y de uno, las cuales, expresan reglas sencillas, siendo esto suficiente para predecir los estados posibles del sistema. A esta idea se le conoce como determinismo laplaciano debido a que fue el matemático Pierre Simon de Laplace quien mejor la expresó cuando afirmó en su Teoría analítica de las probabilidades que si existiera una inteligencia que conociese todas las fuerzas de que está animada la naturaleza, nada sería incierto para ella y el devenir como el pasado, estaría presente ante sus ojos (Madrid, 2011).
Sin embargo, al extenderse el estudio de sistemas dinámicos, surgieron problemas que condujeron al planteamiento de ecuaciones diferenciales no lineales, en las cuales, no existe una proporcionalidad entre causas y efectos, la gran mayoría de ellas no tienen solución analítica y pueden presentar comportamiento caótico. Así, uno de los retos que enfrentaron matemáticos y físicos entre los siglos XVIII y XIX fue el problema de los n cuerpos, el cual, puede enunciarse como sigue: determinar el movimiento en el espacio de n cuerpos con distinta masa y fuerza gravitacional mutua. El problema para n = 2, es decir, para dos cuerpos, fue resuelto primero por Newton, quien utilizó una solución geométrica; posteriormente, Daniel Bernoulli lo resolvió en forma analítica en 1734 y, por último, Euler lo resolvió con lujo de detalle en 1744 (Madrid, 2011).
Una vez resuelto el problema para dos cuerpos, se planteó el problema para n = 3. Esto motivó nuevamente a matemáticos y físicos para hallar una solución. Sin embargo, la naturaleza de este problema era más complicada que la del caso para dos cuerpos ya que no solamente consistía en encontrar las ecuaciones que describen el movimiento de tres cuerpos con distinta masa, ya sea en forma general o específica, sino que, además, en abordar también el problema de la estabilidad del sistema solar. El mismo Newton estaba consciente del problema de la inestabilidad en las órbitas de los planetas. De esta forma, hubo muchos matemáticos y físicos que abordaron este problema a través de dos grandes programas de investigación: el primero, se centró en encontrar soluciones generales al problema de los tres cuerpos, mientras que el segundo se planteó como propósito hallar soluciones específicas a este problema. Nombres como los de Lagrange y Laplace resaltan en abordar el problema de los tres cuerpos. Pero fue el matemático francés Henri Poicaré quien al tratar de resolver este problema encontró indicios de lo que hoy en día se conoce como caos determinista, dando inicio así a un nuevo programa de investigación.
En 1885 el Rey de Suecia y de Noruega Oscar II, quien tenía interés por los problemas de la física y matemática, auspició un concurso con el propósito de resolver en forma definitiva el problema de los tres cuerpos, así como el problema de la estabilidad del sistema solar. Cinco años después de la convocatoria, es decir en 1890, se dieron a conocer los resultados del ganador. Poincaré participó en el concurso a través de su Memoria sobre las curvas definidas por una ecuación diferencial, en la que presentó sus avances sobre sistemas dinámicos lineales y no lineales a través de métodos cualitativos (geométricos y topológicos) destacando que existen cuatro posibles resultados desde el punto de vista de la estabilidad de un sistema dinámico: fuentes, sumideros, puntos silla y centros, atractores válidos para sistemas dinámicos continuos en el plano. Sin embargo, para sistemas de tres dimensiones o más estos resultados no aplican. Así, para el caso del problema de los tres cuerpos, los resultados de Poincaré mostraron que era imposible obtener fórmulas explícitas para describir el movimiento de tres cuerpos celestes. En este contexto, al intentar resolver este problema, Poincaré fue el primero en tratar la posibilidad de la existencia del caos, entendido como la conducta aperiódica que exhibe un sistema determinista y que, depende sensiblemente, de los cambios en los valores numéricos de las condiciones iniciales. Dicho comportamiento, hace que las predicciones de largo plazo sean imposibles de calcular, erosionando así la creencia en el determinismo laplaciano que predominaba en la ciencia de aquella época. Aunque los resultados que presentó Poincaré al comité del concurso no fueron considerados como satisfactorios, fue declarado ganador y fundador de un nuevo programa de investigación para estudiar el problema de la estabilidad del sistema solar. En la siguiente imagen se presenta una línea del tiempo que ilustra la historia del problema de los n cuerpos (Madrid, 2011).
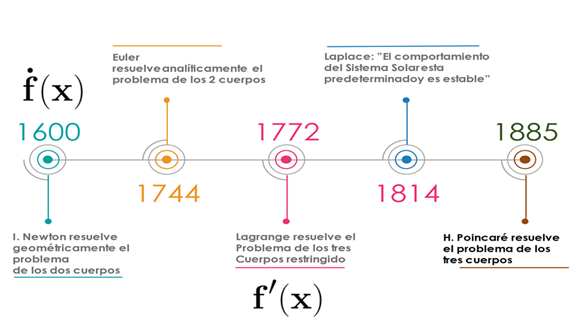
Figura 1. Línea del tiempo: problema de los n cuerpos entre los siglos XVII y XIX. Fuente: Elaboración propia con base en Madrid (2011), La mariposa y el tornado. Colección RBA, España
No obstante, con las relevantes aportaciones de Poincaré, el estudio de los sistemas dinámicos no lineales tuvo su verdadero boom a partir de la década de 1950 gracias a la aparición de las computadoras. La importancia y utilidad de las computadoras reside en que permiten “experimentar”, usando las ecuaciones, de una manera que antes era imposible, contribuyendo así a la comprensión de la dinámica de muchos fenómenos.
Así, Lorentz descubrió en 1963 el movimiento caótico de un atractor mientras estudiaba un modelo de ciclos de convección de la atmósfera. Con su trabajo, encontró que las soluciones de este modelo nunca llegaban al equilibrio o a un estado periódico; por el contrario, continuaban oscilando de forma irregular. Más aún, si comenzaba la simulación con dos condiciones iniciales ligeramente diferentes, pronto se observaban conductas totalmente diferentes, lo cual, sugería que el sistema era inherentemente impredecible, afirmación inaceptable bajo la perspectiva determinista de la ciencia.
Junto a este resultado, Lorentz también encontró que había una estructura en el caos cuando graficó en tres dimensiones las soluciones de su modelo, dando origen a un conjunto de puntos en forma de alas de una mariposa, hoy conocido como “atractor de Lorentz”. Este comportamiento fue explicado como una infinita aglomeración de superficies. A partir de entonces, la cantidad creciente de estudios sobre sistemas dinámicos empezó a cubrir un dominio amplio de fenómenos que, previo al desarrollo de la computación, no era posible cubrir, entre ellos, los fenómenos de la economía y demás ciencias sociales.
De esta forma, el estudio de sistemas dinámicos planteó la posibilidad de desarrollar nuevos métodos en el estudio de la dinámica de los sistemas, lo cual, contribuyó al reconocimiento de la complejidad presente en muchos fenómenos estudiados por las ciencias naturales y sociales. Hoy en día, por ejemplo, se sabe que no es posible predecir el estado del clima más allá de cierta cantidad de tiempo (horas o días). Pero también se sabe que no es posible predecir cuándo ocurrirá el siguiente crash financiero. Uno de los principales aportes de los estudios sobre el caos en estos sistemas consiste, precisamente, en romper con la creencia que prevaleció durante los siglos XVIII, XIX y casi todo el siglo XX en la ciencia: que el conocimiento de las reglas que determinan el comportamiento de un fenómeno implica la posibilidad de predecir su estado futuro en el largo plazo. Por el contrario, estos estudios muestran que conocer estas reglas no implica la capacidad de predicción de los estados en la evolución de un sistema cuando t tiende a infinito, sino que, más bien se acepta cada día más, que el horizonte de predictibilidad es limitado y que el propósito de la ciencia no es hacer predicciones precisas sino prever posibles escenarios con herramientas cualitativas de análisis. En el caso de los sistemas socioeconómicos, la riqueza y variedad en los patrones de comportamiento dinámico no solo confirma su naturaleza impredecible, sino que, además, constituye un reto epistemológico por la diversidad de factores que intervienen en las interacciones que ocurren a partir de las decisiones intencionales de los seres humanos. En suma, la naturaleza es más diversa y rica en su dinámica de lo que se había creído en siglos pasados.
3.1.2 Modelos dinámicos y su clasificación
La dinámica de los fenómenos, naturales o sociales puede ser estudiada cuando se concibe a éstos como un sistema, es decir, como un conjunto de elementos que interactúan entre sí de alguna forma y, a su vez, guardan interacción con otros sistemas que son considerados como su entorno. De esta forma, puede establecerse el sistema dinámico a estudiar. En general, un sistema dinámico se puede definir como aquel sistema cuyo estado queda determinado específicamente por un conjunto de variables y su conducta está predeterminada por reglas (Sayama, 2015). Su modelización matemática se logra cuando los elementos del sistema, sus reglas de interacción y las interacciones de sus elementos con el entorno, se traducen a expresiones algebraicas conocidas como ecuaciones diferenciales.
Ahora bien, hay dos formas para estudiar a un sistema dinámico dependiendo de la manera en que se representa el tiempo. Si el tiempo, t, adopta números reales entonces se dice que el sistema dinámico es continuo, es decir, que evoluciona como si el tiempo transcurriera de manera continua, sin saltos. Se utilizan ecuaciones diferenciales ordinarias para su modelización. Cabe señalar, que las ecuaciones diferenciales ordinarias se clasifican, a su vez, por el orden de la derivada mayor que contienen: si la variable dependiente aparece expresada como segunda derivada, y ésta es la derivada mayor que aparece en la ecuación, entonces se dice que es una ecuación diferencial de orden dos, etc. Sí, además, las ecuaciones diferenciales representan los cambios en el espacio, se llaman ecuaciones diferenciales parciales de orden tal. Por otra parte, si el tiempo, t, se representa con números enteros positivos, incluyendo el cero, entonces se dice que el sistema dinámico es discreto, en el sentido de que el sistema evoluciona en unidades de tiempo que guardan una distancia entre sí, por ejemplo, entre el 1 y el 2 hay una distancia que los separa, ya que no se consideran los números reales que hay entre estos dos números. En este caso, se utilizan las ecuaciones en diferencias finitas para su modelización.
Un segundo criterio de clasificación, se refiere al tipo de hipótesis que representan: si la hipótesis describe una relación lineal entre las variables independiente y dependiente, es decir, una relación proporcional entre ellas, entonces se dice que el sistema es lineal ya que la regla de interacción entre las variables establece una relación de proporcionalidad; por otro lado, si la regla de interacción establece una relación no proporcional entre las variables, lo cual, puede ocurrir si las variables independientes están elevadas a un exponente diferente de cero y mayor que uno, o si se multiplican entre sí, entonces se dice que el sistema es no lineal.
Con base en estos dos criterios se pueden dar combinaciones de tal forma que las ecuaciones diferenciales y en diferencias pueden modelar sistemas que evolucionan en forma lineal o no lineal en el tiempo y en el espacio. Por encima de estas diferencias, los modelos basados en ecuaciones diferenciales o en diferencias comparten el mismo enfoque, es decir, representan la evolución del sistema en términos globales o, dicho de otra forma, a una escala macro. A esto se le conoce como enfoque de arriba hacia abajo (top-down). Así, las variables independiente y dependiente que aparecen en las ecuaciones diferenciales y en diferencias, expresan comportamientos promedio de los elementos que componen el sistema, mientras que los parámetros representan condiciones impuestas por el entorno. Existe otro enfoque que puede complementar el estudio de la dinámica de un sistema y se conoce como enfoque de abajo hacia arriba (bottom up), pero se expone en el capítulo dedicado a modelación basada en agentes. El siguiente cuadro resume esta clasificación.
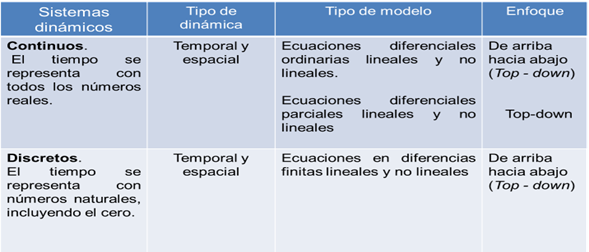
Cuadro 1. Tipos de sistemas dinámicos. Fuente: elaboración propia.
En el siguiente apartado, se presenta en forma detallada el uso de sistemas dinámicos continuos lineales y no lineales.