3.4. Ecuaciones en diferencias
3.4.1 Introducción
El propósito de este apartado es presentar una introducción a las ecuaciones en diferencias con el propósito de mostrar el potencial que tiene esta herramienta en la modelación y estudio de los sistemas complejos de tipo socioeconómico. A diferencia de las ecuaciones diferenciales, las ecuaciones en diferencias consideran los valores del tiempo como valores discretos, es decir, como valores separados por números enteros entre uno y otro. Su principal ventaja reside en que muchos de los fenómenos o procesos naturales y sociales observables, están medidos en unidades de tiempo discreto por lo que su dinámica puede ser estudiada mediante modelos de ecuaciones en diferencias. Algunos ejemplos de estos fenómenos son: el crecimiento económico, la desigualdad socioeconómica, el comportamiento de los mercados, los procesos de elección política, entre muchos otros. Otra ventaja que tiene el uso de ecuaciones en diferencias es que, en la modelación de un fenómeno permite estudiar su evolución con base en distintos valores posibles que pueden adoptar los parámetros, lo que hace posible identificar distintas características en la dinámica de un sistema complejo, por ejemplo, rupturas de simetría o comportamientos que se ubican al borde del caos. En esta introducción se expone el mapeo logístico como un ejemplo de las fases que puede presentar un sistema complejo en su dinámica.
3.4.2 Fenómenos de crecimiento
Los fenómenos de crecimiento son estudiados en distintas áreas de la ciencia: demografía, biología, economía, entre otras. Los modelos matemáticos básicos para llevar a cabo estos estudios parten del problema de describir las pautas del crecimiento de una población, la cual, puede referirse a elementos en distintas escalas de la materia: desde bacterias hasta animales como los mamíferos y las personas.
En la sección de ecuaciones diferenciales se mencionó que el modelo básico para estudiar el crecimiento de una población es el de Verhulst, el cual, se representa con una ecuación diferencial ordinaria no lineal conocida como la ecuación logística, la cual, contiene la hipótesis de Malthus como caso particular que sostiene lo siguiente: una población que no tiene recursos limitados de alimento y espacio, describe un crecimiento exponencial a través del tiempo. Así, la ecuación logística describe el crecimiento de una población en condiciones más realistas al considerar las restricciones dadas por los recursos, es decir, lo que Verhulst llamó la “capacidad de carga” del sistema. En estas condiciones, el crecimiento de una población tiene un límite.
Si bien el modelo de Malthus y el de Verhulst representan las pautas que sigue un fenómeno de crecimiento en unidades de tiempo continuo, muchos de los fenómenos de este tipo miden sus variables en unidades de tiempo discreto, es decir, en valores numéricos que corresponden a unidades de tiempo que se diferencian entre ellas por números enteros, por ejemplo, para medir el crecimiento económico de un país se utiliza el producto interno bruto (PIB) que representa el valor monetario de lo que se produce en un país en unidades de tiempo anuales. Estos valores del PIB están expresados en unidades de tiempo discreto, ya que la distancia temporal que separa los valores del PIB que corresponde al año 2020 y los valores del PIB que corresponde al año 2021 es de una unidad, es decir, de un año. En este caso, no es posible saber el valor del PIB entre 2020 y 2021, por ejemplo, el valor del PIB correspondiente al año 2020.35, ya que el PIB no es una variable medida en unidades de tiempo continuo. De esta forma, existen muchos fenómenos de crecimiento estudiados en distintas áreas de la ciencia donde los valores de las variables están expresados en tiempo discreto. En estos casos, es más adecuado trabajar con ecuaciones en diferencias, sobre todo si el propósito es predecir el valor del estado futuro del sistema.
Pero ¿qué características tiene una ecuación en diferencias? La primera es que los valores numéricos de la variable independiente están dados en unidades de tiempo discreto, como ocurre en el caso de la variable PIB y, por lo tanto, los valores numéricos de la variable dependiente también están dados en unidades de tiempo discreto. La segunda característica consiste en que la solución de la ecuación se obtiene en forma aproximada a través de un proceso iterativo. Un proceso iterativo consiste en partir de un valor inicial de la variable independiente para calcular el primer valor de la variable dependiente, tomar este valor e introducirlo nuevamente a la ecuación para calcular el segundo valor de la variable dependiente y así sucesivamente hasta aproximar la solución de la ecuación a través de un conjunto de puntos. Estas características quedan más claras se revisa el modelo de Malthus y Verhulst, pero en su versión discreta, es decir, usando ecuaciones en diferencias en vez de ecuaciones diferenciales.
3.4.3 El modelo discreto de Malthus
Partamos nuevamente, como en el modelo continuo, de la hipótesis sobre el crecimiento de la población planteado por Robert Malthus, la cual, se expresa de la siguiente forma: resulta razonable esperar que el número de individuos existentes en cualquier instante de tiempo sea proporcional al número de individuos en el instante previo.
Ahora, para expresar esta hipótesis a través de una ecuación en diferencias, se establecen los siguientes símbolos:
Si,
pn, es el número de individuos de la población en el instante n;
n, es un número entero positivo o cero; cuando n = 0 representa el instante inicial;
p0 > 0, es el número de individuos en el instante inicial,
entonces la ecuación:
\(p_{n+1}=\lambda p_n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\right) \)
es una ecuación en diferencias finitas y es el modelo para estudiar el crecimiento de una población con base en la hipótesis de Malthus.
La solución de esta ecuación se obtiene mediante un proceso iterativo de la siguiente forma:
dado el valor de p0, entonces se obtiene el siguiente valor, es decir, el valor de p1 como sigue
\(p_1=\lambda p_0 \)
\(p_2=\lambda p_1=\lambda^2p_0 \)
\(...\ \)
\(p_n=\)
\(\lambda^np_0 \)
La ecuación que resulta de este proceso, es decir, la ecuación:
\(p_n=\lambda^np_0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\right) \)
Es la solución de la ecuación (1). Con base en la ecuación (2) se pueden responder algunas preguntas sobre el crecimiento de una población, por ejemplo: ¿cuáles son las posibilidades de crecimiento de una población? Es posible observar tres posibilidades:
- Si λ > 0, entonces el tamaño de la población, pn, crece hasta infinito.
- Si 0 < λ < 1, entonces el tamaño de la población, pn, disminuye y tiende a cero cuando n tiende a infinito.
- Si λ = 1, entonces el tamaño de la población, pn, es igual al tamaño de la población inicial, p0, para toda n mayor o igual que uno.
Para ilustrar uno de estos escenarios ¿qué pasa con una población si λ = 2 y p0 = 2? ¿Cómo crece una población bajo estas condiciones? Con estos valores, tenemos la ecuación:
\(p_n=2^n2 \)
Si se le asignan valores a n, por ejemplo, n = 0, 1, 2, 3, 4, se obtienen los siguientes datos:
|
Valores de n |
\( p_n=2^n2 \) |
|
0 |
2 |
|
1 |
4 |
|
2 |
8 |
|
3 |
16 |
|
4 |
32 |
Tabla 4. Tamaño de una población conforme n crece Fuente: elaboración propia.
En la Tabla 4 se observa que conforme el valor de n aumenta, el tamaño de la población crece indefinidamente, tal como se indica en el primer inciso. En la siguiente gráfica se observa la tendencia de crecimiento de la población:
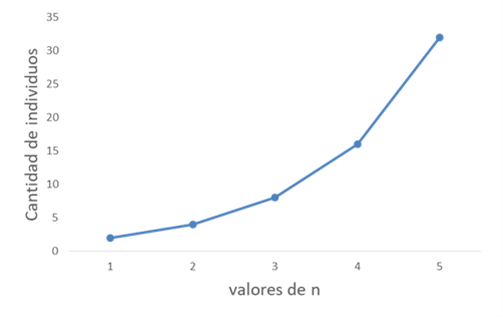
Figura 19. Crecimiento de una población.
La gráfica muestra que, conforme n crece en una unidad, el tamaño de la población crece más que proporcionalmente, lo que describe un crecimiento exponencial como se observa en el modelo en tiempo continuo de Malthus expuesto en la sección anterior.
La limitación principal de este modelo reside en que supone el crecimiento de una población en condiciones poco realistas. Así, a mediados del siglo XIX el matemático belga Pierre François Verhulst (1804-1849) propuso la siguiente hipótesis: los recursos de los que dispone una población (agua, comida, clima, etc.) y, en general el medio en que esta se desarrolla no cambia significativamente, por lo que el número de individuos no puede crecer indefinidamente, las condiciones del medio soportan un número máximo de individuos.
En la sección anterior, se presentó la versión en tiempo continuo de esta hipótesis conocido como el modelo logístico o ecuación logística, la cual, es una ecuación diferencial ordinaria no lineal. En esta sección, se presenta la versión en tiempo discreto, es decir, con una ecuación en diferencias conocido como mapeo logístico.
3.4.4 El modelo discreto de Verhulst
El modelo de Verhulst en su versión discreta o también conocido como mapeo logístico, tiene como base dos hipótesis: la primera, es la hipótesis de Malthus sobre el crecimiento de la población y, la segunda hipótesis, hace referencia al crecimiento restringido de la población cuando se consideran los recursos limitados.
Partiendo de estas hipótesis, es posible establecer el siguiente comportamiento: si N es el número máximo de individuos y, nuevamente, pn es el número de individuos de la población en el instante n mayor o igual que cero, entonces:
- Si pn es mayor que N, entonces pn comienza a decrecer;
- Si pn es menor que N, entonces pn comienza a crecer hasta que se aproxima a N; y si lo rebasa entonces decrece nuevamente.
Este comportamiento del crecimiento de una población se recupera en la siguiente ecuación:
\(p_{n+1}=\lambda p_n\left(1-\frac{p_n}{N}\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(3\right) \)
Donde: N, es el parámetro de aniquilación.
La ecuación (3) es una ecuación en diferencias cuya solución se obtiene utilizando, nuevamente, el proceso iterativo. Otra expresión del mapeo logístico es: si se supone que N es igual a uno y que pn es un valor entre cero y uno, entonces:
\(p_{n+1}=\lambda p_n\left(1-p_n\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(4\right) \)
El mapeo logístico describe, en condiciones más realistas, la dinámica de crecimiento de una población. Sin embargo, esta ecuación guarda una gran riqueza en su dinámica por la variedad de comportamientos incluyendo bifurcaciones y caos, los cuales, son propiedades que presentan muchos sistemas complejos. Estos descubrimientos, se debieron a los estudios de Robert May.
3.4.5 Los sorprendentes descubrimientos de Robert May
El científico australiano Robert May (1936-2020) pionero en el área de biofísica, con base en sus estudios sobre dinámica de población de diversas especies de animales, publicó en 1976 un interesante artículo sobre el comportamiento que presenta el mapeo logístico al ir asignando distintos valores al parámetro λ.
El propósito de May era encontrar un modelo demográfico sencillo que pudiera explicar la dinámica de una población que, conforme transcurre el tiempo, crece más lentamente a medida que se acerca a una cantidad límite de individuos. En esa búsqueda, May se percató de que el mapeo logístico describía adecuadamente la dinámica de una población para ciertos valores del parámetro λ. Sin embargo, para otros valores de λ, existía una gran cantidad de soluciones, las cuales, eran muy distintas entre sí. En algunos casos, las soluciones se alternaban sin converger ni a valores estacionarios ni a soluciones periódicas. El comportamiento aparentemente aleatorio contenido en las soluciones del mapeo logístico para distintos valores de λ, llamaron la atención científica ya que se trata de un modelo determinista sencillo que contiene gran riqueza en la dinámica del sistema. El trabajo de Robert May detonó el interés por el estudio del caos determinista.
El análisis de estabilidad del mapeo logístico muestra inmediatamente la riqueza que contiene en su dinámica para diferentes valores de λ y de la condición inicial p0. De esta forma, si en la ecuación (4) los valores de λ cambian entre cero y cuatro, y los valores de la condición inicial, p0, cambian entre cero y uno, se pueden observar distintos comportamientos que son estables e inestables. La ecuación (4) tiene dos puntos fijos (o puntos de equilibrio): p0* = 0 y \(p_\lambda^\ast=\frac{\lambda-1}{\lambda} \). El análisis de estabilidad para el primer punto fijo se muestra en la siguiente tabla:
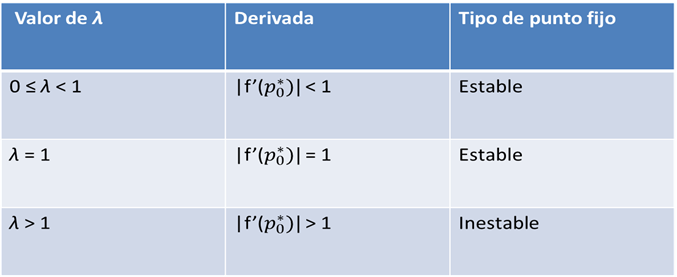
Tabla 5. Análisis de estabilidad para el primer punto fijo del mapeo logístico. Fuente: elaboración propia.
El análisis de estabilidad para el primer punto fijo del mapeo logístico muestra que un pequeño cambio en el valor de λ, esto es, cuando λ es ligeramente mayor que 1, entonces el punto fijo se vuelve inestable. Sin embargo, la mayor diversidad en la dinámica se muestra en el análisis de estabilidad del segundo punto fijo. En la siguiente tabla se muestran los resultados del análisis.
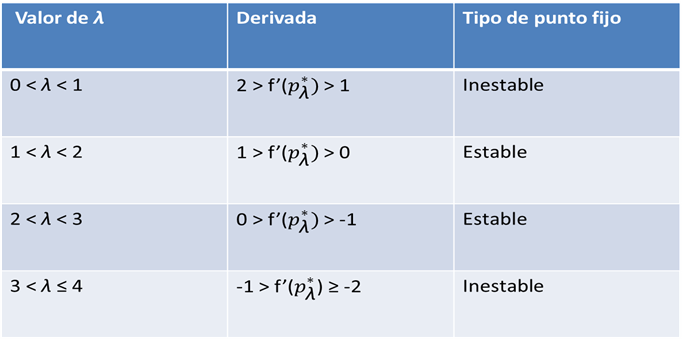
Tabla 6. Análisis de estabilidad para el segundo punto fijo del mapeo logístico Fuente: elaboración propia.
En la Tabla 6, se observa que para diferentes valores de λ entre cero y cuatro, el segundo punto fijo cambia de inestable a estable y de estable a inestable. Estos resultados del análisis de estabilidad se confirman cuando se realiza el mapeo para diferentes valores del parámetro λ y la condición inicial p0. Así, por ejemplo, si λ = 2.9 y con una condición inicial de p0 = 0.1, se obtiene el siguiente mapeo:
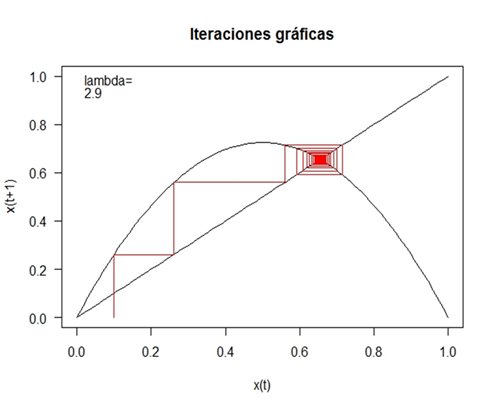
Figura 20. Mapeo para λ = 2.9 y p0 = 0.1.
En la gráfica se observa que para los valores propuestos para el parámetro λ y la condición inicial p0, la trayectoria de la solución converge con el segundo punto fijo o, dicho de otra forma, se confirma que, para estos valores, el segundo punto fijo es estable. Sin embargo, la dinámica cambia en forma radical si el parámetro λ = 4 y la condición inicial es la misma. El resultado se muestra en la siguiente gráfica.
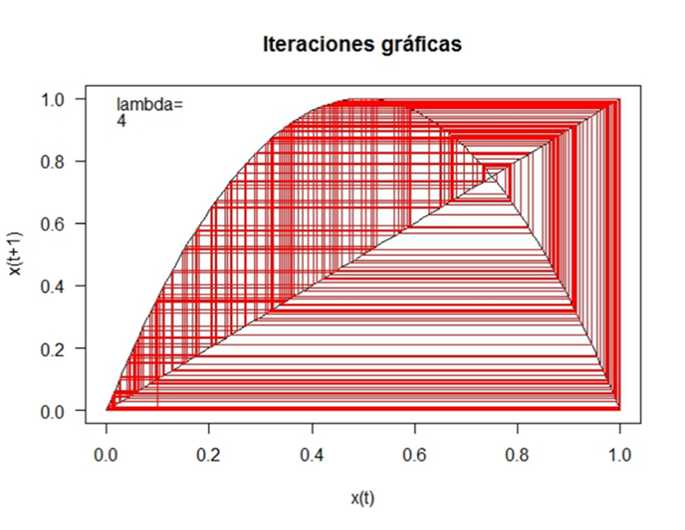
Figura 21. Mapeo para λ = 4 y p0 = 0.1.
En la Figura 21 se observa que cuando varía el valor del parámetro λ y asume un valor de 4 dejando igual el valor de la condición inicial, el segundo punto fijo se vuelve inestable y las trayectorias que describe se comportan en forma errática o aleatoria. En estas condiciones, el sistema se encuentra en régimen caótico.
Otra característica que muestra el mapeo logístico es la sensibilidad ante cambios en la condición inicial, p0. Por ejemplo, para un valor de λ = 3.6785, y modificando ligeramente el valor de la condición inicial p0 = 0.3 a p0 = 0.300001, se observa lo que se muestra en la siguiente gráfica.
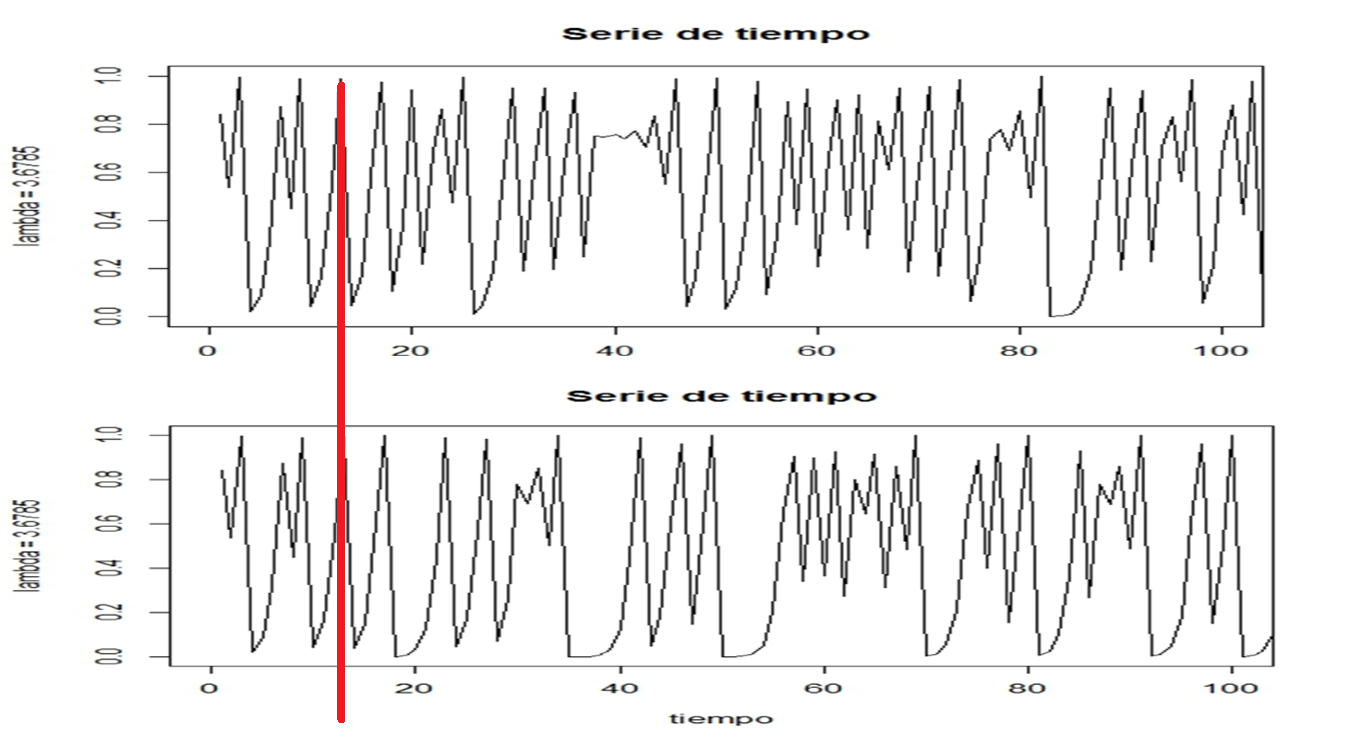
Figura 22. Series de tiempo para λ = 3.6785, p0 = 0.3 y p0 = 0.300001.
En la Figura 22 se observa que, variando ligeramente el valor de la condición inicial y manteniendo constante el valor de λ el comportamiento errático cambia a partir del valor cercano a 20. Aunque los dos comportamientos son erráticos, siguen recorridos distintos.
Ahora bien, si se grafican los valores del parámetro λ entre 2.9 y 4, contra los valores de los puntos de equilibrio, se obtiene el diagrama de bifurcaciones del mapeo logístico.
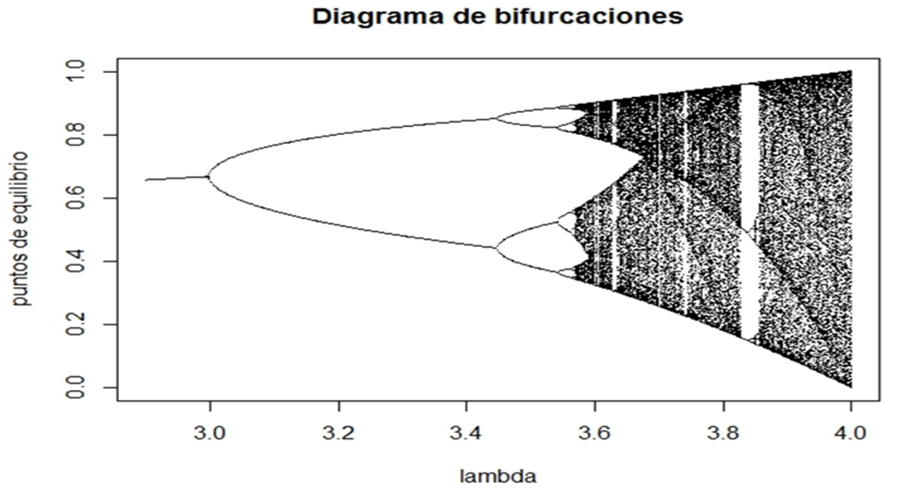
Figura 23. Diagrama de bifurcaciones del mapeo logístico.
El diagrama de bifurcaciones del mapeo logístico muestra la diversidad de dinámicas que tiene el sistema ante cambios en los valores de λ. Así, las líneas continuas representan soluciones estables mientras que las zonas puenteadas representan las soluciones inestables. Los resultados del comportamiento de una población ante distintos valores de λ, se resumen en la Tabla 7.
|
Valores de λ |
Comportamiento de la población |
| \(0<\lambda\le1 \) |
La población termina desapareciendo independientemente del valor inicial. |
| \(1<\lambda\le2 \) |
La población tiende rápidamente al valor (λ-1)/λ, independientemente del valor de la población inicial. |
| \(2<\lambda\le3 \) |
La población tenderá a estabilizarse en (λ-1)/λ, pero antes, fluctúa alrededor de este valor. |
| \(3<\lambda\le1+\sqrt6 \) |
La población oscila casi en todos los casos de valores en la condición inicial. |
| \(3.45<\lambda<3.54 \) |
La población tendrá oscilaciones permanentes aproximándose a cuatro valores. |
| \(\lambda\ ligeramente\ mayor\ que\ 3.54 \) |
La población oscilará entre ocho valores. |
| \(\lambda=4 \) |
La población diverge para casi todos los valores de la población inicial. |
Tabla 7. Comportamiento de una población para distintos valores de λ. Fuente: elaboración propia con base en resultados del mapeo logístico.
Cabe señalar, que en el mapeo logístico la relación entre la longitud de dos intervalos sucesivos de las bifurcaciones se aproxima a la constante de Feigenbaum, es decir, al valor 4.669. Se trata de un periodo doble de bifurcación. Otra característica es que, el diagrama de bifurcación también muestra fractalidad, es decir, que el comportamiento estable e inestable se replica en distintos valores de λ, mostrando que se cumple la propiedad de autosemejanza. En la siguiente gráfica se observa esta propiedad.
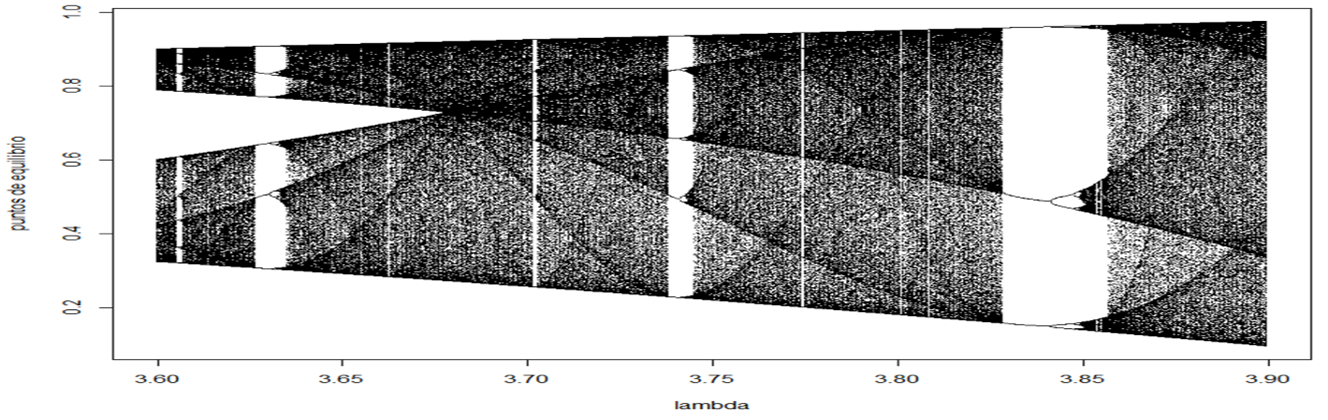
Figura 24. Propiedad de autosemejanza en el diagrama de bifurcación del mapeo logístico.
En la Figura 24, se observa que para distintos valores de λ, se replica el comportamiento observado en la gráfica 4, confirmándose la propiedad de autosemejanza, la cual, es una característica de los fractales.
Otra forma de analizar el comportamiento caótico de un sistema es a través del exponente de Lyapunov, en honor del matemático ruso Aleksandr Mijáilovich Lyapunov (1857-1918) quien contribuyó al estudio de los sistemas dinámicos.
El exponente de Lyapunov (ϒ) es una medida que se utiliza en el análisis de estabilidad de los puntos de equilibrio de un sistema dinámico. Mide la tasa promedio de divergencia o convergencia exponencial de órbitas cercanas. Así, en un sistema caótico las órbitas divergen, en promedio, exponencialmente como . Se puede expresar de la siguiente forma:
\(\Upsilon\left(x_0\right)={lim}_{k\rightarrow\infty}\frac{1}{k}\sum_{i=0}^{k-1}log\left|f^\prime\left(x_i\right)\right| \)
Donde: , es el valor de la condición inicial;
\(f^\prime\left(x_i\right) \), es la derivada de la función estudiada.
Esta expresión, nos dice en qué tasa el valor de la condición inicial se aleja o se acerca de una posición de equilibrio. De esta forma, si , entonces la región del sistema es estable; si , entonces la región del sistema es caótica; y, por último, si entonces la región del sistema presenta bifurcaciones.
Al calcular los exponentes de Lyapunov en el mapeo logístico para valores del parámetro λ que se encuentran entre 2.9 y 4, que es el intervalo donde el mapeo logístico presenta su mayor riqueza dinámica, se observa lo que se muestra en la siguiente gráfica:
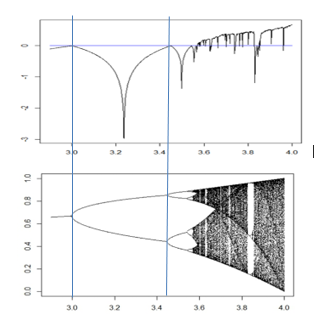
Figura 25. Exponentes de Lyapunov y diagrama de bifurcaciones del mapeo logístico.
En la gráfica se observa cómo coinciden los valores del exponente de Lyapunov con el comportamiento del diagrama de bifurcaciones del mapeo logístico. Así, cuando exponente de Lyapunov es negativo, coincide con las soluciones estables del mapeo logístico, cuando el exponente de Lyapunov es igual a cero, coincide con los puntos de bifurcación y, por último, cuando el exponente es negativo, coincide con el régimen caótico del mapeo logístico.
La riqueza en cuanto a la dinámica que exhibe el mapeo logístico ha llamado la atención no solo de estudiosos en áreas de las ciencias naturales sino también en las ciencias sociales. En la economía se han hecho varias aplicaciones.