En la introducción de este capítulo se mencionó que las ecuaciones diferenciales son una herramienta que ayuda a comprender la dinámica de un sistema en el largo plazo. Para ello, se construye un modelo para describir la evolución en tiempo continuo de los aspectos que interesa estudiar. Esto último, significa que no hay modelos mejores que otros, sino que depende de los propósitos de cada investigación. Además de considerar este aspecto, se sugiere tomar en cuenta los siguientes pasos en la elaboración de un modelo: i) Establecer con claridad las hipótesis en las que se basará el modelo, lo que significa que las relaciones entre las variables a estudiar deben evitar ambigüedades. Un ejemplo de lo que sería una hipótesis especulativa es la afirmación “a los conejos no les preocupa su sobrepoblación”; en contraste, un ejemplo de una hipótesis clara es: “la fuerza es igual a la masa por la aceleración”; ii) Definir las variables y parámetros que se usarán en el modelo, es decir, nombrar las variables independiente y dependiente, los parámetros, las unidades de medida y las escalas a utilizar; iii) Utilizar las hipótesis formuladas en el paso i) para “traducirlas” a símbolos matemáticos y obtener las ecuaciones diferenciales (Blanchard, Devaney, Hall, 1999).
Una vez formuladas las ecuaciones diferenciales, se obtiene su solución con el fin de realizar el análisis dinámico del sistema. Para hallar su solución, se puede utilizar alguno de los siguientes métodos: a) analítico, el cual, consiste en encontrar expresiones matemáticas para los valores futuros de la variable dependiente y, para ello, requiere de técnicas de integración. El problema reside en que no todas las ecuaciones diferenciales se pueden integrar, cuando ocurre esto, se tiene que recurrir al uso de alguno de los otros dos métodos; b) método cualitativo, se apoya en técnicas geométricas que permiten describir la evolución de la variable dependiente en el largo plazo a través de su gráfica; y c) método numérico, que consiste en aproximarse a los valores de la variable dependiente en el largo plazo a través de cálculos aritméticos, para ello, resulta útil el uso de la computadora. Más adelante, se expondrá el uso de estos métodos a través de algunos ejemplos.
Una ecuación diferencial es una ecuación que contiene, por lo menos, una de las derivadas de una función desconocida. En general, tiene la forma:
\(\frac{dx}{dt}=f(x,t)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\right)\)
El lado izquierdo de la expresión significa la derivada o la razón por la cual una cantidad x, cambia con respecto al tiempo ; mientras que el lado derecho representa una función que depende de la cantidad x y del tiempo, t. Así, la ecuación que involucra una función desconocida y sus derivadas se llama ecuación diferencial. La solución de una ecuación diferencial consiste entonces en hallar la función desconocida.
Las ecuaciones diferenciales permiten modelar sistemas dinámicos continuos, es decir, sistemas en los que su evolución a través del tiempo está determinada por variables que modifican su valor en unidades de tiempo continuo (sin saltos), y reglas determinadas.
Para mostrar la modelización de un sistema dinámico continuo con ecuaciones diferenciales, se presenta el siguiente ejemplo sencillo: el modelo de Malthus sobre el crecimiento poblacional.
Thomas Robert Malthus (1766-1834), fue un pastor anglicano a cargo de la parroquia de Albury, es conocido por sus aportes a la economía, en particular por su teoría sobre la renta, y también por sus estudios sobre el crecimiento de la población al publicar su Ensayo sobre el principio de la población en 1798. En su Ensayo señala que la población está limitada necesariamente por los medios de subsistencia pero que, si no existe restricción alguna en cuanto a estos medios, entonces la población crece en forma ilimitada, específicamente, la población se dobla cada veinticinco años.
A esta afirmación sobre el crecimiento de la población se le conoce como la hipótesis de Malthus y se puede formular de la siguiente forma: en condiciones ilimitadas de recursos,
No se pierda de vista que esta afirmación sostiene que la tasa de cambio de una población solo depende del tamaño de ésta, es decir, que las limitaciones de espacio o recursos no tienen ningún efecto sobre el crecimiento de la población.
Ya que se tiene claro el significado de la hipótesis, el segundo paso sugerido para plantear un modelo es “traducir” la hipótesis en símbolos matemáticos que expresen una ecuación diferencial. Para ello, se requiere establecer antes las variables y parámetros implicados. De esta forma, si:
P = población (variable dependiente);
t = tiempo (variable independiente); y
k = constante de proporcionalidad (parámetro)
las unidades dependen de la aplicación específica que se realice, por ejemplo, si se modela el crecimiento de moho en un pan, entonces t se puede medir en días y P en el área cubierta por el moho. En caso de que modele el crecimiento de la población mexicana en los Estados Unidos, entonces t se puede medir en años y P en millones de personas. Para fijar el tiempo de inicio, hacemos corresponder t = 0 con el valor del tiempo seleccionado, por ejemplo, 2000 si se desea estudiar el crecimiento de la población mexicana en los Estados Unidos a partir de este año en adelante.
Una vez establecidas las variables, parámetros y unidades o escalas de medición, se puede proceder a “traducir” la hipótesis planteada en una ecuación diferencial. De esta forma, como la velocidad de crecimiento de la población es dP/dt y, como señala la hipótesis, ésta es proporcional al tamaño de la población, es decir, a kP, entonces tenemos que la expresión:
\(\frac{dP}{dt}=kP\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\right)\)
Representa la hipótesis planteada. De acuerdo con la clasificación de las ecuaciones diferenciales presentada en la introducción, se trata de una ecuación diferencial lineal, porque la variable P está elevada a la potencia 1 y no a potencias superiores. Por este motivo, también la ecuación expresa que hay una relación de proporcionalidad entre el tamaño de P y su velocidad de crecimiento, es decir, que las causas son proporcionales a los efectos. El orden de la ecuación es 1, ya que aparece la primera derivada de P respecto de t. Por último, como no hay derivadas parciales, entonces se trata de una ecuación diferencial lineal ordinaria de orden uno.
Ahora bien, una vez planteado el modelo, se requiere encontrar su solución, es decir, encontrar la ecuación que satisface la primera derivada de P respecto de t, dP/dt. Para ello, se utiliza alguno de los métodos señalados: cualitativo, analítico o numérico.
El método cualitativo se vale de técnicas geométricas y analíticas para explorar el comportamiento de las posibles soluciones de una ecuación diferencial. Este método adquiere importancia al menos por dos aspectos: cuando las ecuaciones diferenciales no tienen solución analítica o exacta, lo cual ocurre en la mayoría de los modelos dinámicos no lineales, se puede tener una idea aproximada de las gráficas de las posibles soluciones y cómo se comportan alrededor de las posiciones de equilibrio; y con esta información es posible prever posibles escenarios y, en dado caso, tomar decisiones.
En el caso del modelo de Malthus, la ecuación diferencial sí tiene solución analítica o exacta, pero suponiendo que no la tuviera, se podría explorar el posible comportamiento de las soluciones de la siguiente forma.
Llámese condición inicial al valor inicial de la población, es decir, al valor de la población en el tiempo t = to = 0. Así, este valor inicial de la población se puede representar como: P(t = to = 0) = Po. Ahora bien,
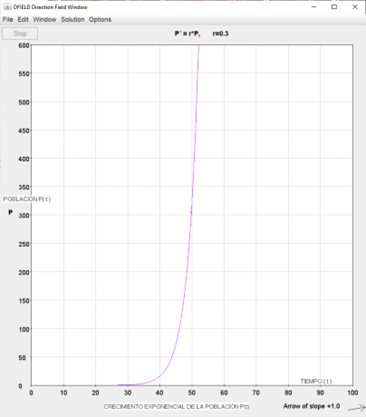
Figura 2. Crecimiento exponencial de P(t).
Ahora bien, por cada condición inicial, es decir, para cada valor inicial de la población P(0), se obtiene una función P(t) distinta, tal como se observa en la Figura 3.
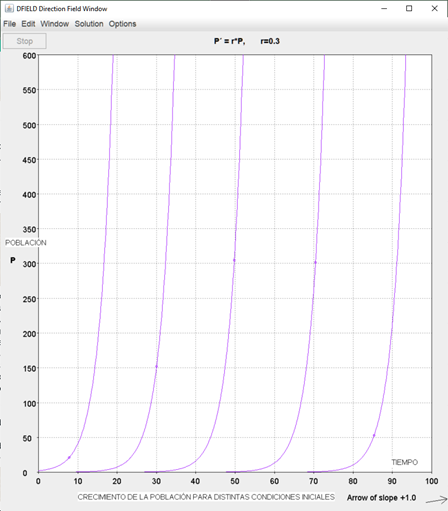
Figura 3. Crecimiento exponencial de P(t) para varias condiciones iniciales.
En la Figura 3, también se observa que si P(0) < 0 y siendo k > 0, entonces \(\frac{dP}{dt}<0\) , para todo t = 0, por lo que P(t) disminuye, y al crecer t P(t) se vuelve más negativa. Desde el punto de vista del fenómeno estudiado, este comportamiento se puede omitir ya que no tiene sentido hablar de “población negativa”. Con este análisis se puede afirmar que el modelo de Malthus predice comportamientos explosivos de la población, siempre y cuando P(0) > 0.
Este análisis exploratorio sobre el comportamiento de las posibles soluciones se puede complementar con una técnica cualitativa conocida como el campo de pendientes. Se trata de una técnica geométrica que consiste en hallar las pendientes de las rectas tangentes en los puntos sobre la gráfica de una función solución, en este caso P(t), de la cual, se desconoce su expresión específica.
Para aplicar esta técnica es necesario considerar la forma de la ecuación diferencial. Si la ecuación diferencial es no autónoma, es decir, de la forma:
\(\frac{dx}{dt}=f\left(t,x\right)\)
Donde t aparece explícitamente como una variable independiente, el campo de pendientes mostrará que, para cada coordenada, esto es, para cada par de puntos (t, x), se tiene una pendiente distinta de la recta tangente a la curva de la gráfica de las soluciones de la ecuación. El caso es distinto para ecuaciones diferenciales autónomas, con la forma:
\(\frac{dx}{dt}=f\left(x\right)\)
Donde t no aparece, en forma explícita, como una variable independiente. En este caso, el campo de pendientes es paralelo a lo largo de cada línea horizontal, ya que: f (t1, x) = f (t2, x) = f (x).
El modelo de Malthus es una ecuación diferencial autónoma, por lo que el campo de pendientes corresponde a este último caso, tal como se muestra en la Figura 4:
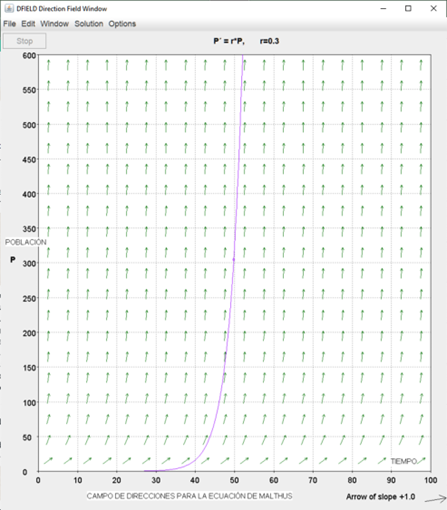
Figura 4. Campo de pendientes de la ecuación de Malthus.
La gráfica de la Figura 4, confirma la forma de las gráficas de cada solución particular de la ecuación diferencial (1) inferido en el análisis anterior. Por último, para complementar este análisis utilizaremos la línea-fase para saber algo acerca de la dinámica de las soluciones alrededor de la posición de equilibrio P(t) = 0.
Por lo tanto, se puede concluir que la posición de equilibrio, P(t) = 0, es una fuente.
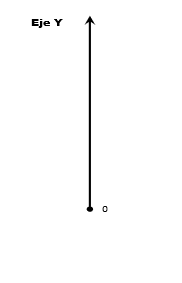
Figura 5. Línea-fase del modelo de Malthus.
El método analítico consiste en encontrar una solución específica de una ecuación diferencial. Su importancia reside en que, con esta ecuación, es posible predecir los estados futuros del sistema dinámico, por lo menos bajo cierto horizonte temporal. Sin embargo, implica encontrar la función integral correspondiente a la ecuación diferencial, lo cual, en muchos casos no es posible.
De esta forma, si se conoce el valor exacto de Po, es decir, de la condición inicial P(0), y se desea predecir algún valor de la población, entonces se requiere la expresión precisa de la función P(t). A esto se le conoce como problema de condiciones iniciales y se plantea de la siguiente forma:
\(\frac{dP}{dt}=kP,\ \ \ \ \ \ \ \ \ \ \ \ P\left(0\right)=Po\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\right)\)
Para solucionarlo, se requiere hallar una función P(t) cuya derivada sea el producto de k con P(t), es decir, se necesita encontrar su función integral. Para ello, se puede usar un método conocido como método de separación de variables, que consiste en separar las variables dependientes de las variables independientes para hallar la integral. En este caso:
\(\frac{dP}{dt}=kP\)
Separando variables,
\(\frac{dP}{P}=kdt\)
Integrando y evaluando,
\(\int_{Po}^{P}{\frac{dP}{P}=k\int_{0}^{t}dt}\)
\(LnP-LnPo=k\left(t-0\right)\)
Utilizando una propiedad de los logaritmos,
\(Ln\left(\frac{P}{Po}\right)=kt\)
Aplicando la función exponencial,
\(\frac{P}{Po}=e^{kt}\)
Despejando a P, se obtiene finalmente,
\(P\left(t\right)=Poe^{kt}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(3\right)\)
Que es la solución al problema de condiciones iniciales (2). La expresión (3) confirma que, conforme aumenta t, la población, P(t), crece en forma exponencial. Obsérvese su utilidad con un ejemplo específico.
Supóngase los siguientes datos hipotéticos sobre la población mexicana en Estados Unidos (ver Tabla 1).
Años
T
Valor real (datos hipotéticos)
Valor que arroja el modelo
1960
0
1.5
1970
10
2.1
1980
20
2.9
1990
30
4.2
2000
40
6.3
2010
50
7.6
8
2020
60
8.4
11.2
Tabla 1. Población de mexicanos en Estados Unidos (millones de personas). Fuente: elaboración propia con base en datos hipotéticos.
Sea el problema de condiciones iniciales,
\(\frac{dP}{dt}=kP,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P\left(0\right)=1.5\)
Con \(P\left(t\right)=1.5e^{kt}\), como solución. Para calcular los valores para otros momentos del tiempo con base en el modelo de Malthus, se requiere calcular el valor de k. Para ello, se toma el valor de P(10), es decir, el segundo valor de P que aparece en el cuadro 2. De esta forma,
\(2.1=1.5e^{k\left(10\right)}\)
Despejando a e, se tiene que:
\(e^{k\left(10\right)}=\frac{2.1}{1.5}\)
Aplicando logaritmo natural, se obtiene:
\(10k=\ln{\left(\frac{2.1}{1.5}\right)}\)
Resolviendo el logaritmo y despejando a k, se obtiene que:
\(k\approx0.03364\)
Por lo tanto, la solución al problema de condiciones iniciales planteado es
\(P\left(t\right)=1.5e^{0.03364t}\)
Al utilizar los cálculos para t = 0, t = 10, …, t = 60, se obtienen los resultados que arroja el modelo y que aparecen en la última columna del cuadro 2. Al contrastarlos con los datos reales sobre la población de mexicanos en los Estados Unidos (datos hipotéticos), se observa que los cinco primeros datos que arroja el modelo de Malthus corresponden a los datos reales, lo cual, muestra la capacidad de predicción del modelo. Sin embargo, a partir del sexto dato, los datos que arroja el modelo se separan más de los datos reales conforme pasa el tiempo. Ver la Figura 6.
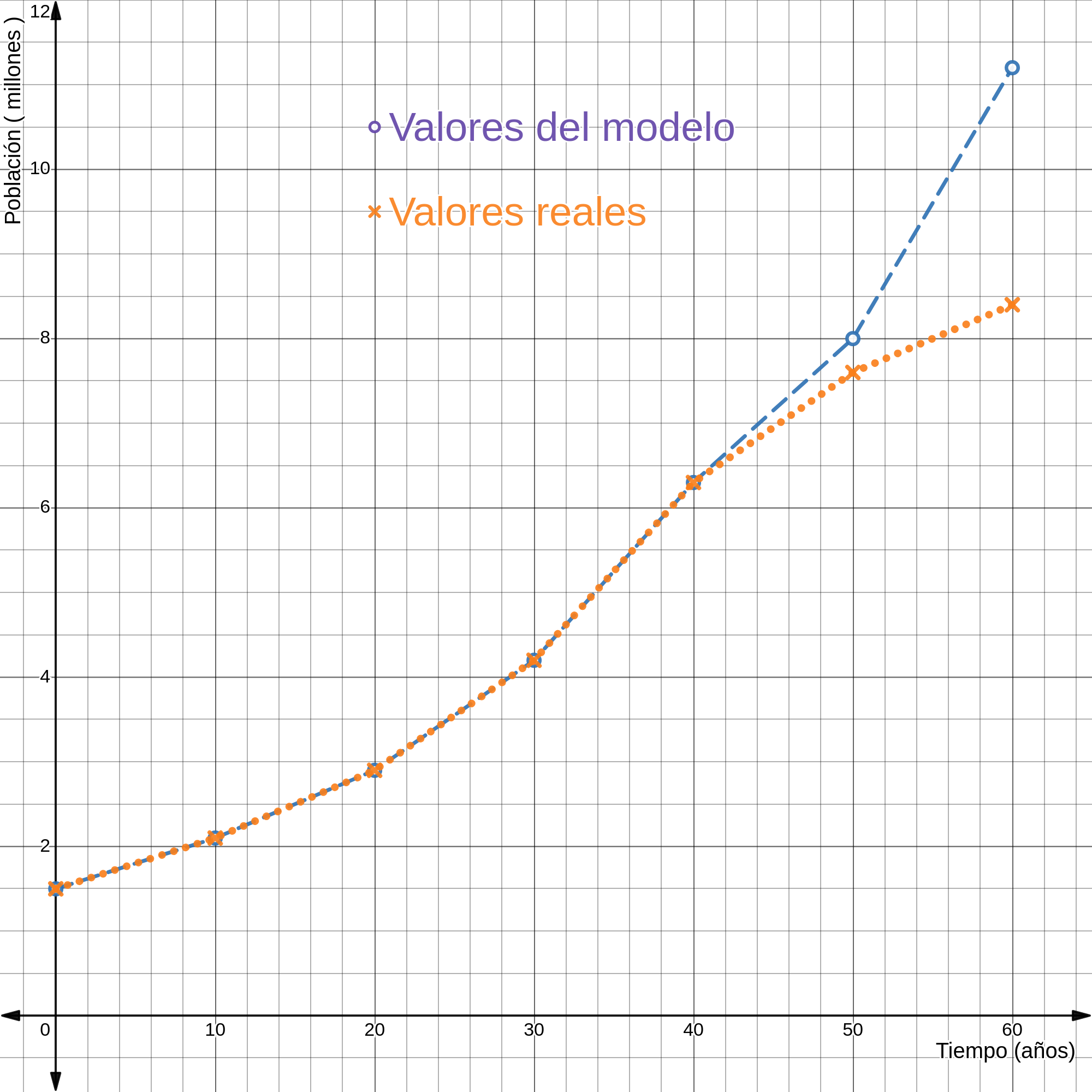
Figura 6.
Esto último, se debe a que el modelo fue construido a partir de una hipótesis que no considera otros posibles factores que pueden influir en el crecimiento de la población mexicana en los Estados Unidos. Así, al incorporarse dichos factores, se daría lugar a otras hipótesis que darían origen a otro modelo más sofisticado sobre el crecimiento de la población. En la siguiente sección se revisará otro modelo un poco más sofisticado que el de Malthus. Lo importante por el momento, es resaltar el hecho de que la solución analítica de una ecuación diferencial permite hacer predicciones exactas bajo cierto horizonte temporal, ahí reside su importancia.
El análisis numérico ofrece un conjunto de métodos que permiten aproximar soluciones de ecuaciones diferenciales, sin hallar su solución exacta. Esto tiene como ventaja dos aspectos: i) aproximarse a las soluciones de ecuaciones diferenciales que no se pueden resolver en forma analítica; y ii) que, hoy en día, esto se puede llevar a cabo en forma rápida con el uso de las computadoras. La desventaja es, precisamente, que se obtienen aproximaciones de las soluciones y no soluciones exactas. Esto hace imposible la predicción, pero sí es posible llevar a cabo un análisis cualitativo de los posibles resultados. Con el propósito de ilustrar, se explica a continuación en qué consiste el método más sencillo conocido como el método de Euler.
El método de Euler fue propuesto por el matemático y físico suizo Leonhard Euler (1707-1783) entre los años 1768 y 1770 en su obra Institutionum calculi integralis. El método consiste en los siguientes pasos:
A manera de ejemplo, considérense los datos del problema de condiciones iniciales visto en el ejemplo anterior. Es decir,
\(\frac{dP}{dt}=kP,\ \ \ \ \ \ \ \ \ \ \ \ \ \ P\left(0\right)=1.5,\ \ \ \ \ \ \ \ \ \ \ \ \ con\ k\approx0.03364 \)
Se fija el tamaño del paso, por ejemplo, ∆t = 10.
El punto inicial es (to, Po) = (0, 1.5).
Se calcula el siguiente punto:
Ct1 = 0 + 10 P1 = 1.5 + (0.05046)10
t1 = 10 P1 = 1.5 + 0.5046
P1 = 2
Por lo tanto, (t1, P1) = (10, 2).
Se repite el proceso para calcular los puntos que siguen. En la Tabla 2 se muestran los cálculos para siete puntos.
k
tk
Pk
(tk, Pk)
(0, 1.5)
1
2
(10, 2)
2.6
(20, 2.6)
3
3.5
(30, 3.5)
4
4.6
(40, 4.6)
5
6.2
(50, 6.2)
6
8.2
(60, 8.2)
Tabla 2. Algunos puntos estimados por el método de Euler para un problema de condiciones iniciales del modelo de Malthus Fuente: elaboración propia.
Al comparar los datos obtenidos con el método de Euler con los datos obtenidos con la solución analítica del modelo de Malthus, se observa que hay un margen de error usando el método de Euler. Sin embargo, este margen de error se reduciría si el tamaño del paso, ∆t, fuera suficientemente pequeño. En la siguiente gráfica se observa la diferencia entre los valores calculados con el método de Euler y los calculados con la solución analítica, la brecha entre ambas gráficas representa el margen de error.
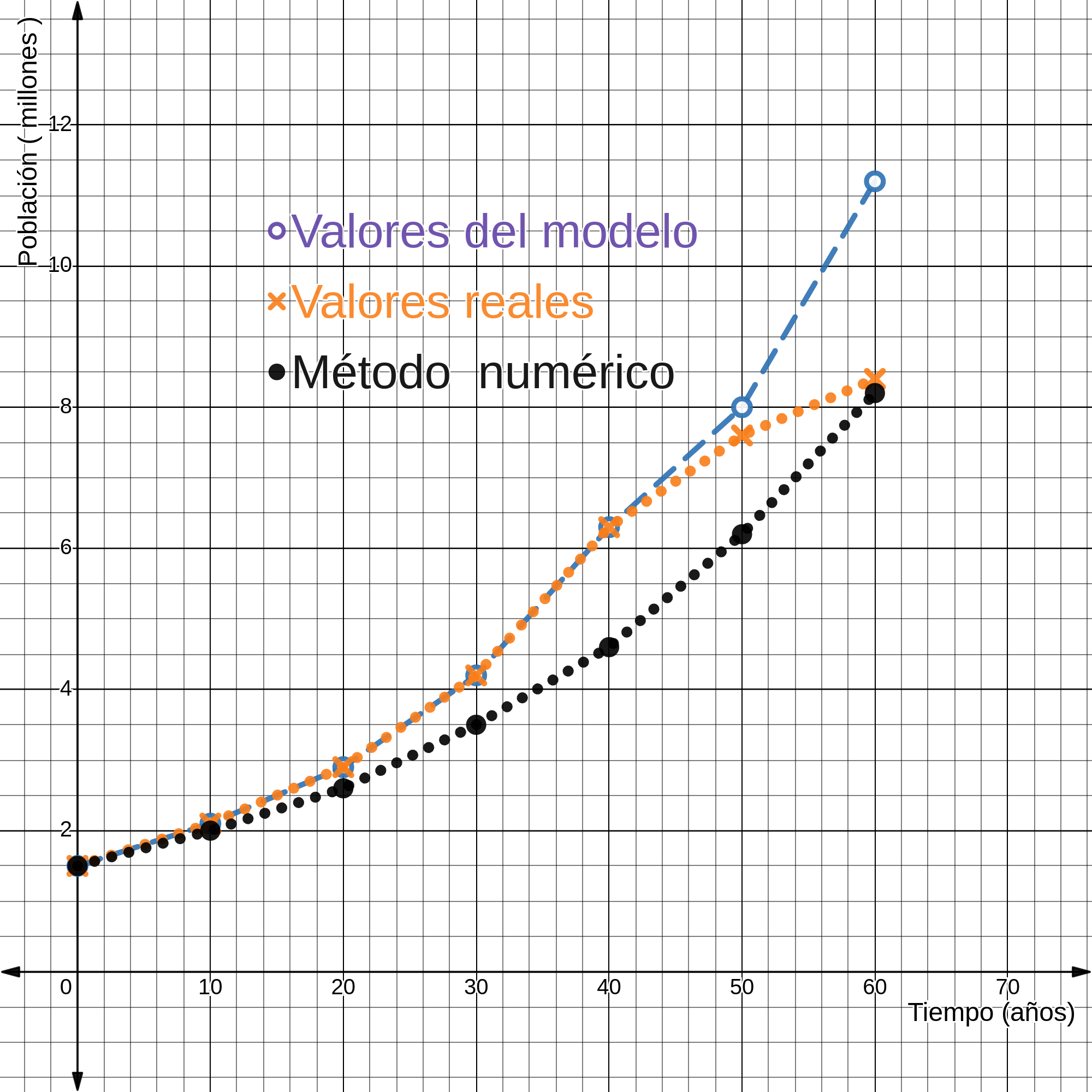
Figura 7.
Si bien el método de Euler ofrece aproximaciones burdas, es la base de otros métodos más sofisticados que se utilizan usando la computadora, por ejemplo, el de Runge-Kutta. De hecho, todas las gráficas del plano-fase que se presentan en este capítulo usan métodos más sofisticados. Sin embargo, el uso de estos métodos se complica en los modelos dinámicos no lineales.
Si bien el modelo de Malthus predice el crecimiento de una población pequeña en cortos periodos de tiempo, no describe adecuadamente cómo crece una población en el largo plazo. La principal limitación que presenta el modelo de Malthus consiste en que no considera el entorno y los recursos limitados bajo los cuales ocurre el crecimiento de una población. Fue el matemático belga Pierre-François Verhulst (1804-1849) quien, con base en estadísticas demográficas, planteó la importancia de factores que frenan el crecimiento de una población en un trabajo que presentó en 1838. Así, el modelo de Verhulst parte de las siguientes hipótesis:
\(\frac{dP}{dt}\approx kP\) , si P es pequeña
Sin embargo, la segunda hipótesis incorpora la expresión “demasiado grande” para referirse a tamaños de población que han rebasado los recursos dados bajo los cuales crece la población. Esta expresión se puede simbolizar como N, el cual, es un parámetro que representa el tamaño de población máxima que pueden soportar los recursos dados por el entorno donde crece la población, o simplemente se le puede identificar como la “capacidad de carga” del sistema. De esta forma, la segunda hipótesis queda como:
\(Si\ P>N,\frac{dP}{dt}<0 \)
Dónde: P, es la población (variable dependiente)
k, es el coeficiente de la razón de crecimiento de la población para poblaciones pequeñas;
N, es la “capacidad de carga”;
t, es el tiempo (variable independiente).
Al combinar las hipótesis el modelo de Verhulst queda de la siguiente forma:
\(\ \ \frac{dP}{dt}=k\left(1-\frac{P}{N}\right)P\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(3\right) \)
La ecuación (3) muestra que el crecimiento de la población en el tiempo ocurre tal y como se establece en las hipótesis. Así, cuando la población, P, está muy por debajo del nivel de población que corresponde a la capacidad de carga, N, de tal manera que el cociente P/N es casi cero, entonces la parte que está entre paréntesis tendrá un valor cercano a 1, por lo que el crecimiento de la población será como lo establece el modelo de Malthus, es decir, exponencial, ya que los recursos son abundantes en esa fase. Sin embargo, en el caso extremo, cuando la población, P, está por encima del nivel que establece la capacidad de carga, N, entonces la parte que esta entre paréntesis tendrá un valor negativo, por lo que la población disminuirá conforme pase el tiempo, lo cual, tiene sentido ya que una población que crece por encima de los recursos que le ofrece su entorno, tendrá que disminuir con el tiempo. Y, por último, cuando la población, P, es igual al nivel de población que establece la capacidad de carga, N, entonces la parte que está entre paréntesis será cero por lo que dP/dt será igual a cero, lo que significa que la población permanece constante a través del tiempo, no crece ni disminuye.
Lo que sigue es buscar la solución de la ecuación (3) utilizando algunos de los métodos que ya se revisaron para solucionar el modelo de Malthus. En este caso, hay que considerar que el modelo de Verhulst es una ecuación diferencial ordinaria no lineal, ya que la variable P se halla elevada al cuadrado. Un problema que presentan las ecuaciones diferenciales no lineales es que no siempre se pueden solucionar por el método analítico ya que no existe la integral de la función, pero se puede hacer una aproximación a su solución en forma cualitativa. A continuación, se presenta una exploración cualitativa de la solución del modelo de Verhulst.
Obsérvese que la ecuación (3) puede escribirse como:
\(\frac{dP}{dt}=f\left(P\right)=k\left(1-\frac{P}{N}\right)P \)
Se puede obtener información cualitativa sobre las soluciones de la ecuación (3) si sabemos cuándo dP/dt es cero, dónde es negativa y dónde es positiva. Si se grafica la función f(P) se puede observar que corta al eje de las abscisas P en dos puntos: P = 0 y P = N, tal y como se muestra en la gráfica de la Figura 8.
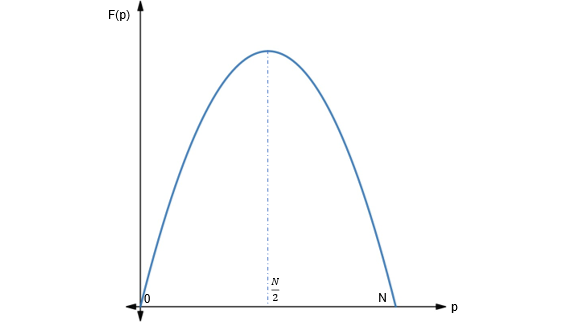
Figura 8 gráfica de f(P).
En la gráfica se observa que cuando P = 0 y P = N, el comportamiento de la población a través del tiempo, dP/dt, es igual a cero, por lo que la población, P, permanece constante a través del tiempo, t. Esto significa que P(t) = 0 y P(t) = N son soluciones de la ecuación diferencial (3). De esta forma, si la población, P, es igual a cero, permanecerá en cero en forma indefinida, y si la población, P, coincide con el valor de la población que corresponde a la capacidad de carga, N, entonces la población, P, ni crecerá ni disminuirá a través del tiempo. Entonces se puede afirmar que P(t) = 0 y P(t) = N son puntos de equilibrio o, dicho de otra forma, son soluciones de equilibrio.
Ahora bien, con base en este análisis cualitativo se puede configurar una idea de cómo son las soluciones en el largo plazo. Por ejemplo, si la población inicial, P(0) se ubica entre 0 y N, se observará que f(P) > 0, en este caso, la tasa de crecimiento de la población a través del tiempo es positiva, dP/dt = f(P) > 0 y, por lo tanto, la población, P(t), está creciendo. Sin embargo, conforme la población, P, se acerque a N, la tasa de crecimiento de la población a través del tiempo, dP/dt = f(P), se acercará a cero, por lo que se espera que la población, P, se nivele con N cuando se acerca a N, tal como se observa en la Figura 9.
Figura 9. Gráfica del plano fase con una condición inicial de P entre 0 y N.
En el caso en que la condición inicial, P(0), esté por encima de N, entonces la tasa de crecimiento a través del tiempo de P, dP/dt, será negativa, lo que significa que la población, P, disminuirá conforme pase el tiempo y se nivelará con N, tal como se observa en la gráfica anterior para niveles de P(0) por encima de N.
Por último, para niveles de P(0) negativos, se observa que P decrece haciéndose más negativa conforme pasa el tiempo. Sin embargo, este comportamiento no tiene sentido ya que no se puede hablar de cantidades negativas de población; en términos del fenómeno estudiado no tiene sentido y, por lo tanto, se puede omitir este comportamiento. Este análisis cualitativo del modelo de Verhulst se confirma con la solución analítica de la ecuación (3) que, por fortuna, existe. A continuación, se presenta la solución del modelo de Verhulst por el método analítico.
Para solucionar en forma analítica el modelo de Verhulst, se plantea primero el problema de condiciones iniciales:
\(\frac{dP}{dt}=k\left(1-\frac{P}{N}\right)P,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P\left(0\right)=Po\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(4\right) \)
Y utilizamos el método de integración conocido como separación de variables, mismo que aplicamos para solucionar el modelo de Malthus.
Obsérvese que:
\(\frac{dP}{dt}=k\left(1-\frac{P}{N}\right)P=kP-\frac{k}{N}P^2 \)
Ahora, separando variables se obtiene:
\(\frac{dP}{\left(1-\frac{P}{N}\right)P}=kdt \)
Aplicando integral, se tiene:
\(\int{\frac{dP}{\left(1-\frac{P}{N}\right)P}=k\int d t} \)
Para integrar una función con fracciones, se utiliza el método de fracciones parciales. La integral queda reescrita de la siguiente forma:
\(\int{\left(\frac{1}{P}+\frac{\frac{1}{N}}{1-\frac{P}{N}}\right)dP=k\int d t} \)
Y esto es igual a,
\(\int_{Po}^{P}{\frac{dP}{P}+\int_{Po}^{P}{\frac{\frac{dP}{N}}{1-\frac{P}{N}}=k\int_{0}^{t}dt}} \)
Evaluando, se obtiene:
\(lnP-lnPo-ln\left|1-\frac{P}{N}\right|+ln\left|1-\frac{Po}{N}\right|=kt \)
Aplicando una propiedad de los logaritmos, se tiene que:
\(\ln{\left(\frac{P}{Po}\right)}+\ln{\left(\frac{1-\frac{Po}{N}}{1-\frac{P}{N}}\right)}=kt \)
Usando otra propiedad de los logaritmos, la expresión anterior queda de la siguiente forma:
\(n\frac{P}{Po}\left(\frac{1-\frac{Po}{N}}{1-\frac{P}{N}}\right)=kt \)
Aplicando la función exponencial:
\( \frac{P}{Po}\left(\frac{1-\frac{Po}{N}}{1-\frac{P}{N}}\right)=e^{kt} \)
Despejando a P, se obtiene:
\( P\left(t\right)=\frac{Poe^{kt}}{1+\frac{Po}{N}\left(e^{kt}-1\right)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(5\right) \)
Que es la solución del modelo de Verhulst.
La ecuación (5) confirma el comportamiento de las soluciones señalado en el análisis cualitativo a través de tres casos límite:
De esta forma, se observa que, para una población inicial, Po, que se encuentra entre 0 y N, la solución describe un comportamiento en forma de “S” alargada, que muestra el comportamiento del tamaño de la población conforme se acerca al valor de N. Por otro lado, cuando la población inicial, Po, se halla por encima de la población permitida por la capacidad de carga, N, se observa que la población decae hasta alcanzar el valor de N, tal como se observa en la Figura. 10.
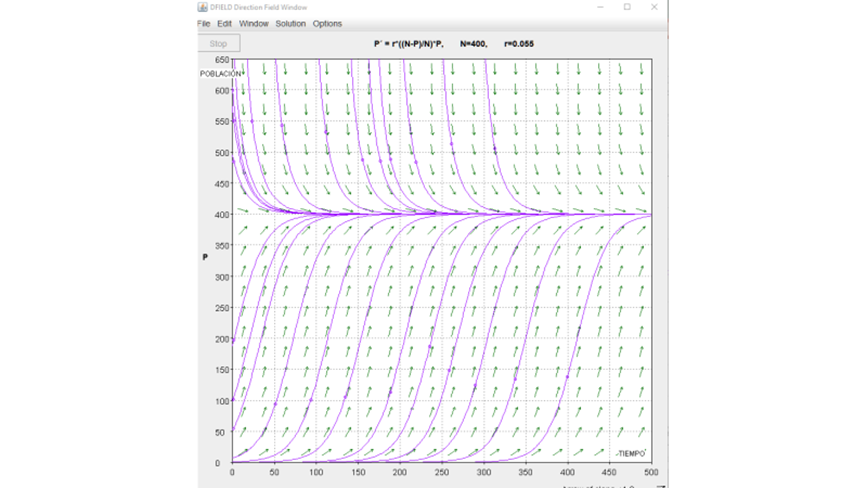
Figura 10. Gráfica de la ecuación logística.
Por último, cabe señalar la importancia que tiene el modelo de Verhulst: es la base para explicar la evolución de poblaciones en demografía; pero también tiene muchas otras aplicaciones en otras áreas de la ciencia como en biología, epidemiología, economía, etc. Se trata de un modelo paradigmático para explicar fenómenos de crecimiento y de difusión. A continuación, se presenta un ejemplo de su aplicación para el caso de la población de los Estados Unidos.
t
Población observada
Población calculada
N=350 Po=3.9
1790
3.9
1800
5.3
5.4
1810
7.2
7.5
1820
9.6
10.4
1830
12.9
14.5
1840
17.1
19.9
1850
23.2
27.3
1860
70
31.4
37.1
1870
80
38.6
49.8
1880
90
50.2
66.0
1890
100
62.9
85.9
1900
110
76.0
109.6
1910
120
92.0
136.3
1920
130
106.5
165.1
1930
140
123.2
194.5
1940
150
132.0
222.7
1950
160
151.8
248.5
170
180.7
271.0
180
205.1
289.6
190
227.2
304.6
200
249.6
316.3
210
282.2
325.31
220
309.3
332.0
230
329.5
336.9
Tabla 3. Estados Unidos: población en millones de personas.
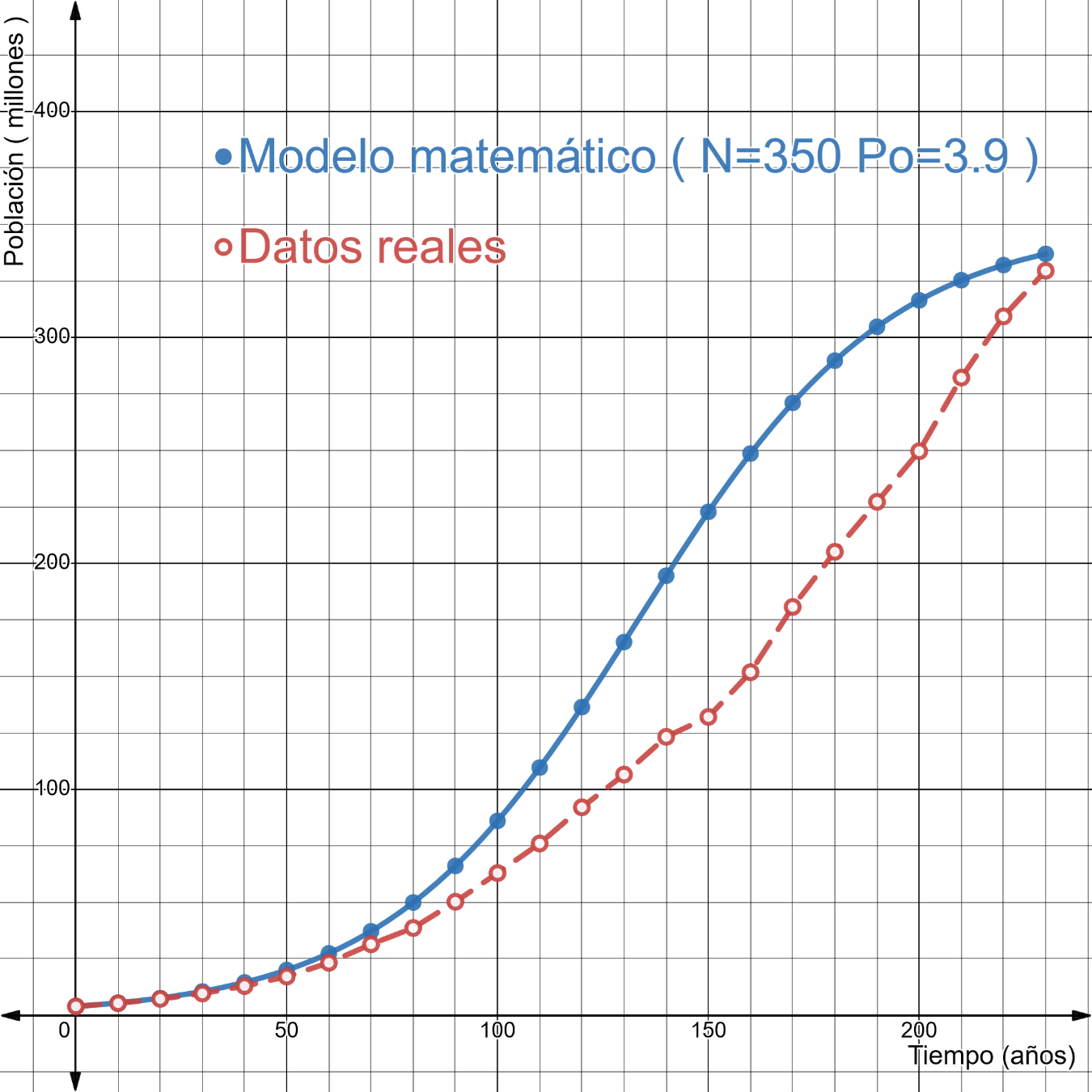
Figura10 Población calculada y población observada.
Si bien el modelo de Verhulst considera los recursos proporcionados por el entorno como un factor que condiciona el crecimiento de una población, no considera otro factor importante: la interacción entre especies; en particular, cuando una especie “se come” a la otra.
El antecedente histórico de este tipo de modelos se halla en las investigaciones realizadas por Volterra y D’ Ancona durante la Primera Guerra Mundial, quienes lo utilizaron con éxito para explicar el incremento en la población de tiburones (depredador) y el decrecimiento de la población de peces (presa) en el mar Mediterráneo.
Para ejemplificar este modelo, supóngase que se tienen dos especies: conejos, que se identifican como “presas”, y zorros, que se identifican como “depredadores”. El modelo se construye a partir de las siguientes hipótesis:
Ahora considérense los siguientes símbolos para plantear el modelo. Sean: C, la población de conejos, y Z, la población de zorros, las variables dependientes; t, la variable independiente; α, el coeficiente de la razón de crecimiento de conejos; β, la constante de proporcionalidad que mide el número de interacciones conejos-zorros en las que el conejo es devorado; γ, el coeficiente de la razón de muertes de zorros; δ, la constante de proporcionalidad que mide el beneficio a la población de zorros de un conejo devorado. Los parámetros α, β, γ, δ, son positivos.
Con base en las hipótesis, el modelo presa-depredador es:
\(\frac{dC}{dt}=\alpha C-\beta CZ \)
(6)
\(\frac{dZ}{dt}=-\gamma Z+\delta CZ \)
El sistema de ecuaciones (6) es un sistema de ecuaciones diferenciales ordinarias de primer orden no lineales acopladas, ya que las razones de cambio de C y Z dependen tanto de C como de Z. La primera ecuación expresa las hipótesis i) y ii). De esta forma, si los conejos no tienen encuentros con los zorros, es decir, cuando βCZ = 0, entonces la población de conejos crece en forma ilimitada; pero si hay encuentros, entonces al crecimiento ilimitado se resta βCZ. La segunda ecuación, considera las hipótesis iii) y iv). Así, cuando no hay encuentros entre zorros y conejos, la razón de cambio de la población de zorros decae en forma proporcional a la población de zorros, es decir, en γZ; pero cuando hay encuentros entre zorros y conejos, se suma δCZ ya que la población de zorros crece.
La solución del sistema de ecuaciones (6) implica, a diferencia de los modelos de Malthus y Verhulst, hallar simultáneamente dos funciones, C(t) y Z(t), que describen las poblaciones de conejos y de zorros en función del tiempo. Desafortunadamente, en este caso no existe la solución analítica, por lo que se tiene que resolver a través del método cualitativo, echando mano de algunos elementos de geometría y análisis.
En general, para describir las trayectorias de la solución de un sistema de dos ecuaciones diferenciales no lineales como el sistema (6), se procede realizando los siguientes pasos:
Aplicando estos pasos en el sistema (6), se obtiene:
Las ecuaciones se igualan a cero y se arreglan de la siguiente forma:
\(C\left(\alpha-\beta Z\right)=0 \)
\(Z\left(-\gamma+\delta C\right)=0 \)
Existen dos posibilidades para que se cumpla la igualdad:
\( \left(\begin{matrix}\alpha-\beta Z&-\beta C\\\delta Z&-\gamma+\delta C\\\end{matrix}\right)=\left(\begin{matrix}\alpha&0\\0&-\gamma\\\end{matrix}\right)\ \)
\(\lambda_1=\alpha\)
Como α y γ son números reales y uno es positivo y el otro negativo, se concluye que el punto de equilibrio P1(0,0) es un punto silla.
\( \left(\begin{matrix}\alpha-\beta Z&-\beta C\\\delta Z&-\gamma+\delta C\\\end{matrix}\right)=\left(\begin{matrix}0&-\beta\frac{\gamma}{\delta}\\\delta\frac{\alpha}{\beta}&0\\\end{matrix}\right)\)
Al calcular los eigenvalores con el polinomio característico, se obtienen números imaginarios puros de la forma: , es decir, con parte real igual a cero. Por lo tanto, se concluye que el punto P2(γ/δ, α/β) es un centro, esto es, con trayectorias cerradas a su alrededor.
Este análisis sobre la estabilidad alrededor de los puntos de equilibrio del sistema presa-depredador, ofrece una idea de cómo son las trayectorias alrededor de éstos, tal como se observa en el plano-fase siguiente:
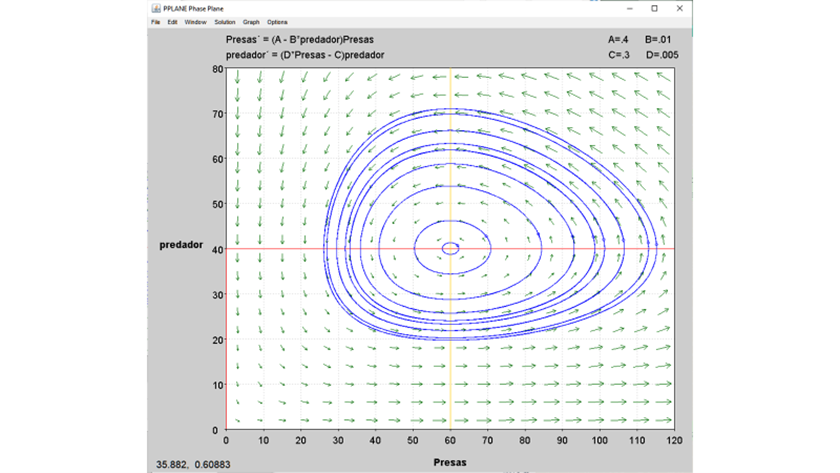
Figura 11. Gráfica del plano-fase del modelo presa-depredador hecha en p-plane.
De acuerdo con el fenómeno modelado, las trayectorias muestran un comportamiento muy interesante, ya que indica que las poblaciones de presas y depredadores oscilan en forma periódica, con periodo y amplitud, que depende de las condiciones iniciales. De esta forma, cuando crece la población de zorros, al transcurrir el tiempo, disminuye la población de conejos poniéndose en riesgo de desaparecer; sin embargo, no desaparece, ya que, al disminuir la población de conejos, también disminuye la población de zorros lo que, a su vez, permite la recuperación de la población de conejos al transcurrir cierto tiempo. Así, emerge un patrón simbiótico que, finalmente, conserva a ambas especies de tal forma que, en promedio, los tamaños de ambas poblaciones se mantienen en los valores de equilibrio C = γ/δ, Z = α/β.
Por último, cabe señalar que el modelo depredador-presa se ha aplicado en distintas áreas de la ciencia, por lo que resulta un sistema paradigmático entre la gama de modelos para estudiar la dinámica de sistemas. En particular, fue utilizado en la economía por Richard M. Goodwin para estudiar la dinámica del ciclo económico con distribución del ingreso entre dos clases sociales. Hoy en día, el modelo del ciclo económico de Goodwin es uno de los más representativos para comprender las pautas bajo las cuales evoluciona una economía capitalista dentro de la perspectiva de la teoría económica poskeynesiana. Más adelante se expondrá con detalle este modelo.